- Introduction
- Theory
- Censoring definition in a data set
- PK data below a lower limit of quantification
- PK data below a lower limit of quantification or below a limit of detection
- PK data below a lower limit of quantification and PD data above an upper limit of quantification
- Combination of interval censored PK and PD data
- Case studies
Objectives: learn how to handle easily and properly censored data, i.e. data below (resp. above) a lower (resp.upper) limit of quantification (LOQ) or below a limit of detection (LOD).
Projects: censoring1log_project, censoring1_project, censoring2_project, censoring3_project, censoring4_project
Introduction
Censoring occurs when the value of a measurement or observation is only partially known. For continuous data measurements in the longitudinal context, censoring refers to the values of the measurements, not the times at which they were taken. For example, the lower limit of detection (LLOD) is the lowest quantity of a substance that can be distinguished from its absence. Therefore, any time the quantity is below the LLOD, the “observation” is not a measurement but the information that the measured quantity is less than the LLOD. Similarly, in longitudinal studies of viral kinetics, measurements of the viral load below a certain limit, referred to as the lower limit of quantification (LLOQ), are so low that their reliability is considered suspect. A measuring device can also have an upper limit of quantification (ULOQ) such that any value above this limit cannot be measured and reported.
As hinted above, censored values are not typically reported as a number, but their existence is known, as well as the type of censoring. Thus, the observation (i.e., what is reported) is the measurement
if not censored, and the type of censoring otherwise.
We usually distinguish between three types of censoring: left, right and interval. In each case, the SAEM algorithm implemented in Monolix properly computes the maximum likelihood estimate of the population parameters, combining all the information provided by censored and non censored data.
Theory
In the presence of censored data, the conditional density function needs to be computed carefully. To cover all three types of censoring (left, right, interval), let be the (finite or infinite) censoring interval existing for individual i at time
. Then,
$$\displaystyle p(y^{(r)}|\psi)=\prod_{i=1}^{N}\prod_{j=1}^{n_i}p(y_{ij}|\psi_i)^{1_{y_{ij}\notin I_{ij}}}\mathbb{P}(y_{ij}\in I_{ij}|\psi_i)^{1_{y_{ij}\in I_{ij}}}$$
where
$$\displaystyle \mathbb{P}(y_{ij}\in I_{ij}|\psi_i)=\int_{I_{ij}} p_{y_{ij}|\psi_i} (u|\psi_i)du$$
We see that if is not censored (i.e.
), its contribution to the likelihood is the usual
, whereas if it is censored, the contribution is
.
For the calculation of the likelihood, this is equivalent to the M3 method in NONMEM when only the CENSORING column is given, and to the M4 method when both a CENSORING column and a LIMIT column are given.
Censoring definition in a data set
In the dataset format used by Monolix and PKanalix, censored information is included in this way:
- The censored measurement should be in the OBSERVATION column.
- In an additional CENSORING column, put 0 if the observation is not censored, and 1 or – 1 depending if the measurement given in the observation column is a lower or an upper limit.
- Optionally, include a LIMIT column to set the other limit.
To quickly include censoring information to your dataset by using BLQ tags in the observation column, you can use data formatting.
Examples are provided below and here.
PK data below a lower limit of quantification
Left censored data
- censoring1log_project (data = ‘censored1log_data.txt’, model = ‘pklog_model.txt’)
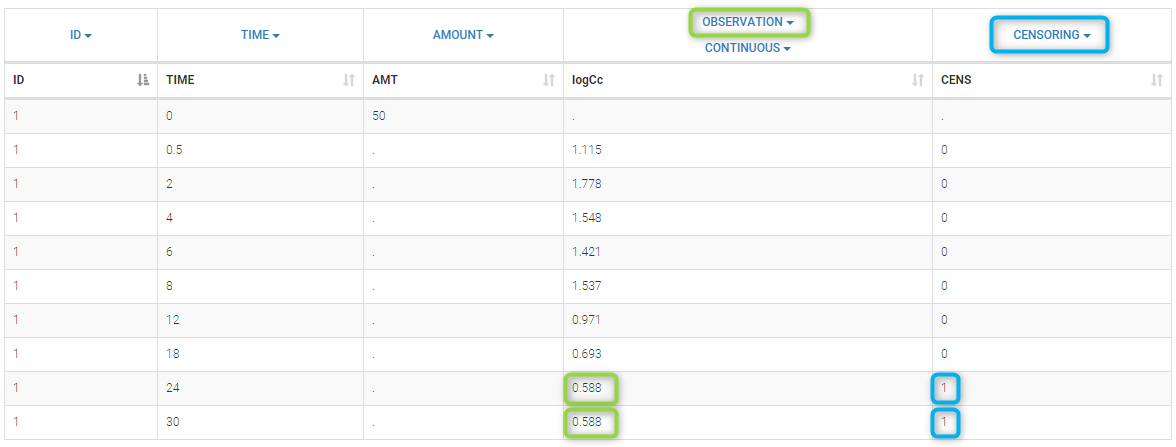
PK data are log-concentration in this example. The limit of quantification of 1.8 mg/l for concentrations becomes log(1.8)=0.588 for log-concentrations. The column of observations (Y) contains either the LLOQ for data below the limit of quantification (BLQ data) or the measured log-concentrations for non BLQ data. Furthermore, Monolix uses an additional column CENSORING to indicate if an observation is left censored (CENS=1) or not (CENS=0). In this example, subject 1 has two BLQ data at times 24h and 30h (the measured log-concentrations were below 0.588 at these times):
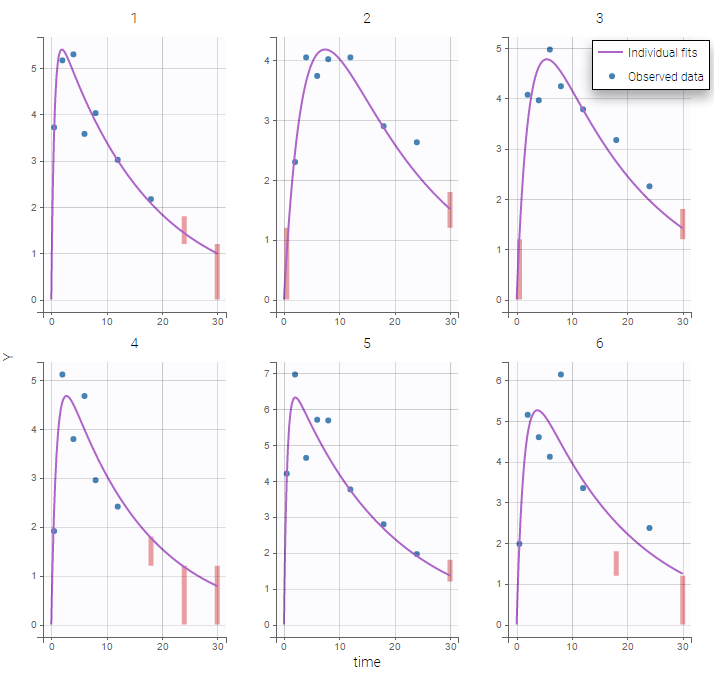
The plot of individual fits displays BLQ (red band) and non BLQ data (blue dots) together with the predicted log-concentrations (purple line) on the whole time interval:
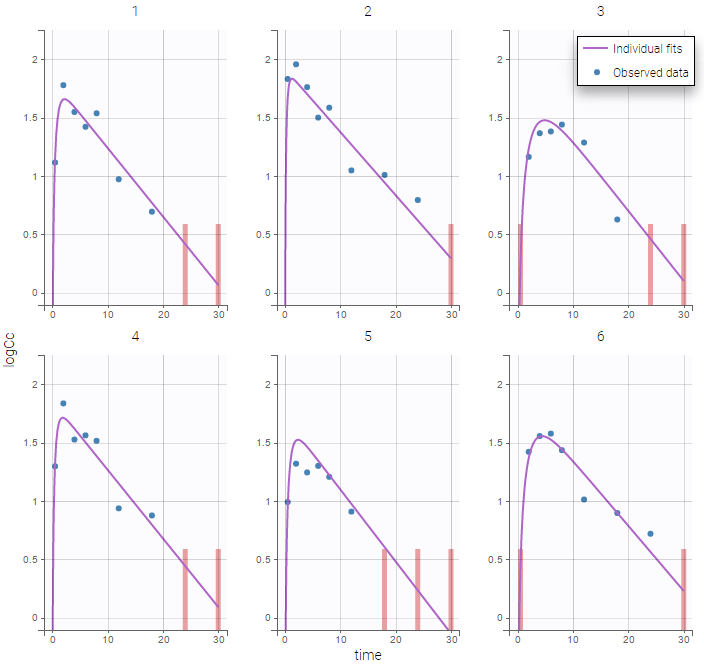
Notice that the band goes from .8 to -Infinity as no bound has been specified (no LIMIT column was proposed).
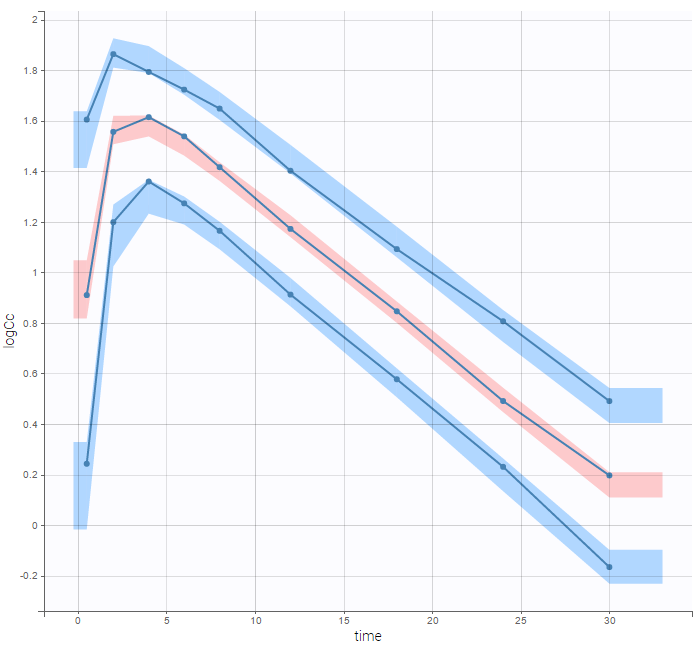
For diagnosis plots such as VPC, residuals of observations versus predictions, Monolix samples the BLQ data from the conditional distribution
$$p(y^{BLQ} | y^{non BLQ}, \hat{\psi}, \hat{\theta})$$
where and
are the estimated population and individual parameters. This is done by adding a residual error on top of the prediction, using a truncated normal distribution to make sure that the simulated BLQ remains within the censored interval. This is the most efficient way to take into account the complete information provided by the data and the model for diagnosis plots such as VPCs:
A strong bias appears if LLOQ is used instead for the BLQ data (if you choose LOQ instead of simulated in the display frame of the settings) :
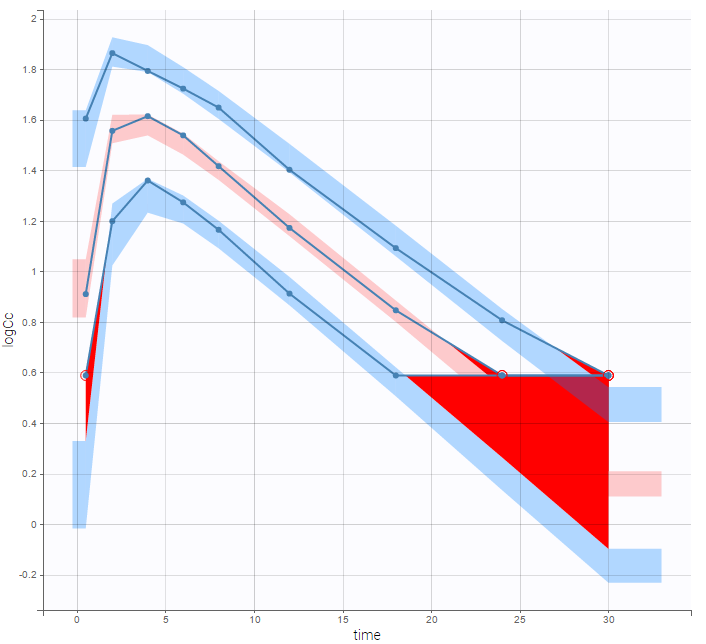
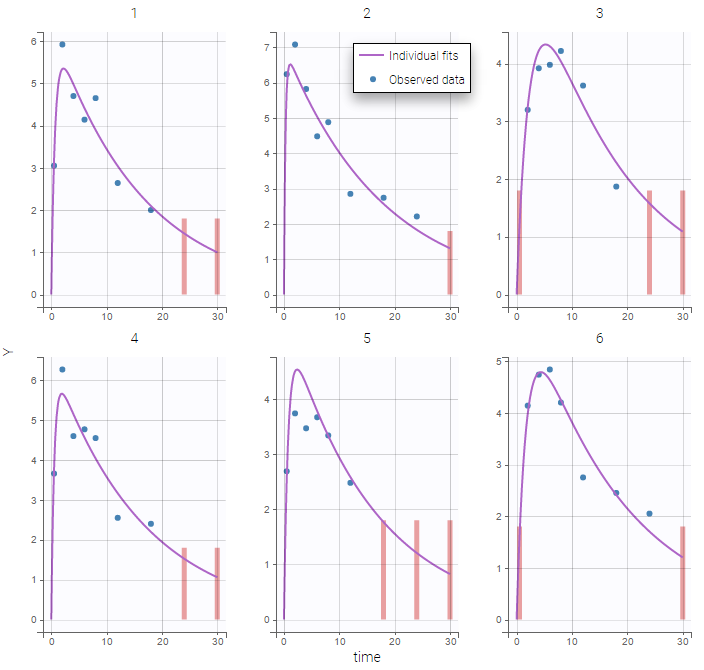
Notice that ignoring the BLQ data entails a loss of information as can be seen below (if you choose no in the “Use BLQ” toggle):
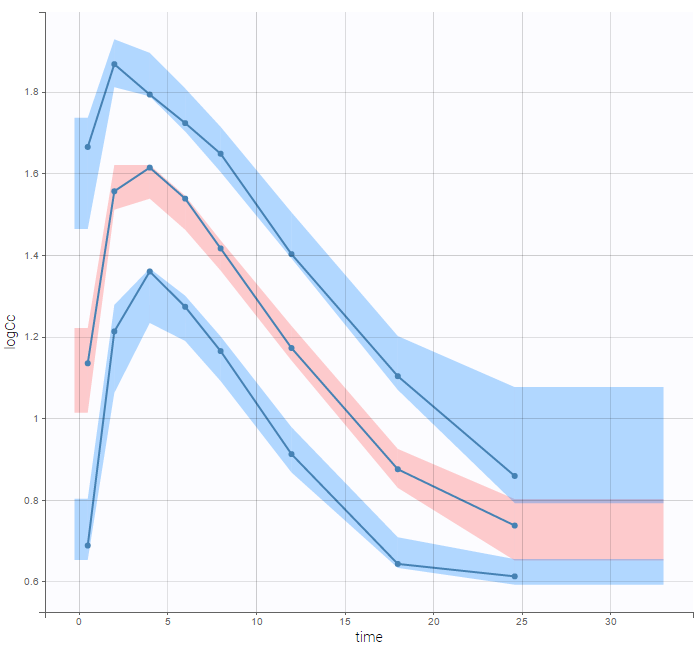
As can be seen below, imputed BLQ data is also used for residuals (IWRES on the left) and for observations versus predictions (on the right)
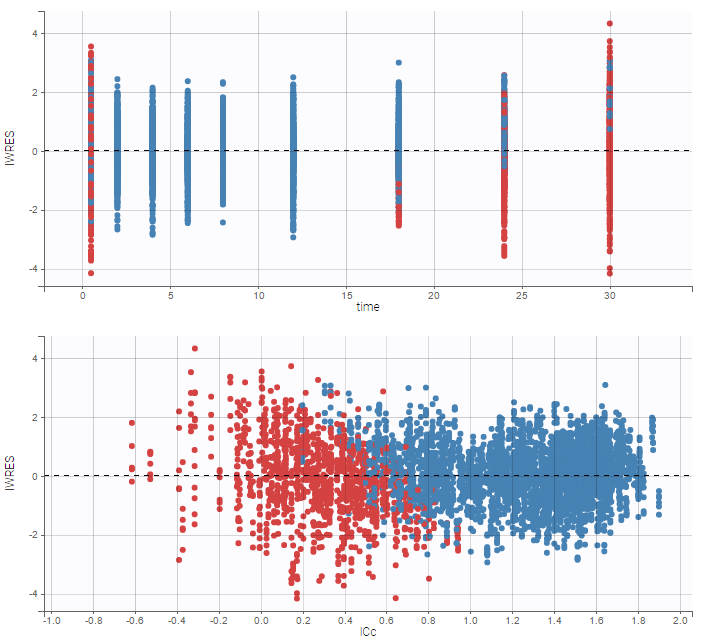 |
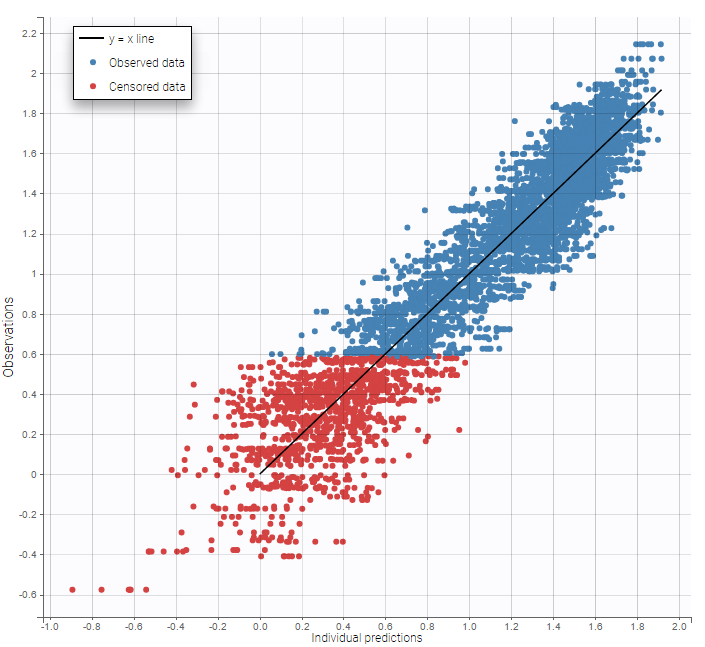 |
|---|
More on these diagnosis plots
Impact of the BLQ in residuals and observations versus predictions plots
A strong bias appears if LLOQ is used instead for the BLQ data for these two diagnosis plots:
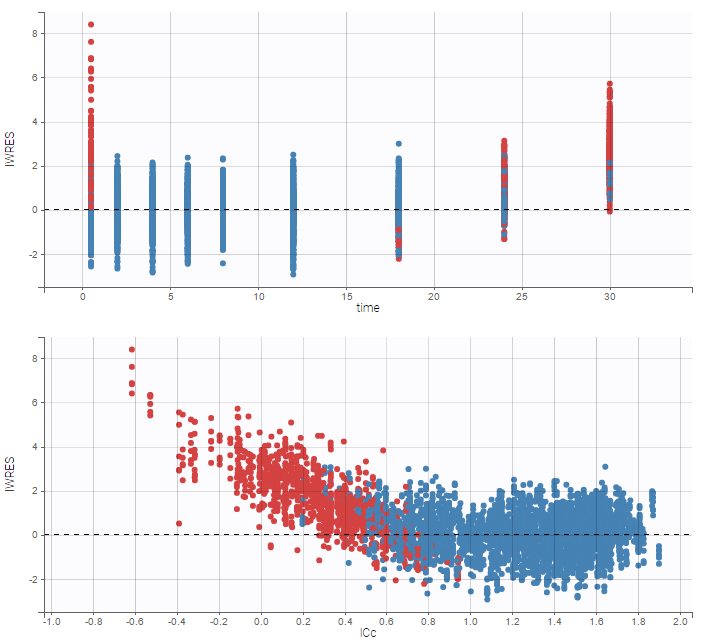 |
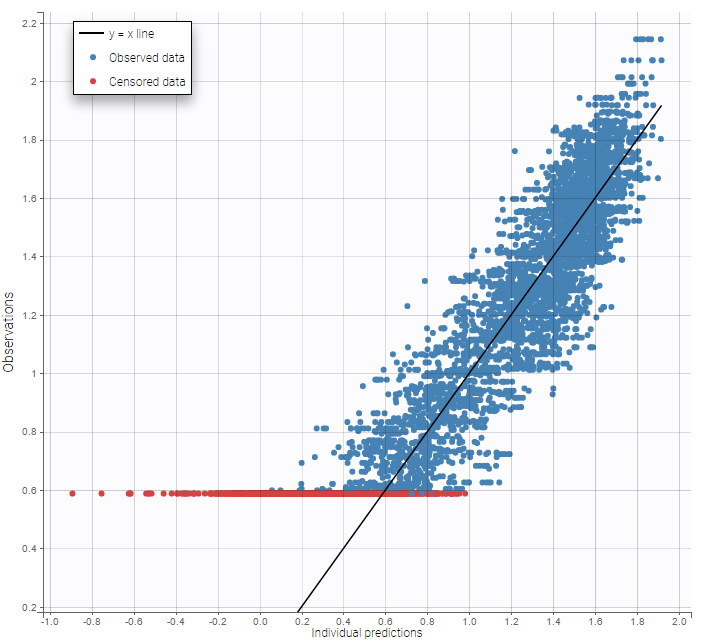 |
|---|
while ignoring the BLQ data entails a loss of information:
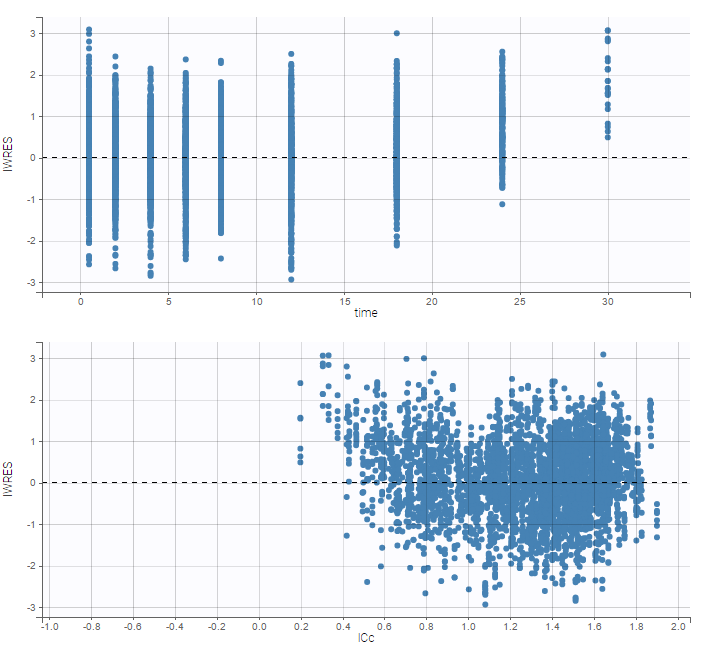 |
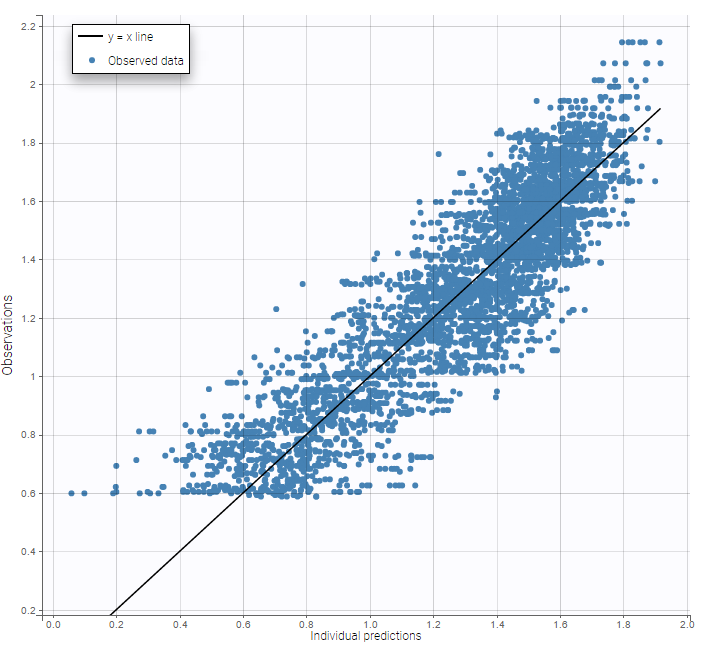 |
|---|
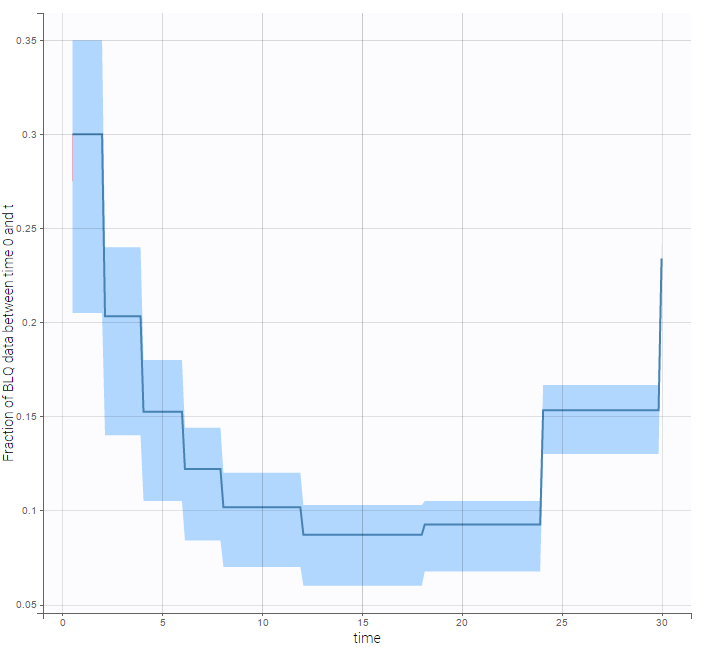
BLQ predictive checks
The BLQ predictive check is a diagnosis plot that displays the fraction of cumulative BLQ data (blue line) with a 90% prediction interval (blue area).
Interval censored data
- censoring1_project (data = ‘censored1_data.txt’, model = ‘lib:oral1_1cpt_kaVk.txt’)
We use the original concentrations in this project. Then, BLQ data should be treated as interval censored data since a concentration is know to be positive. In other word, a data reported as BLQ data means that the (non reported) measured concentration is between 0 and 1.8mg/l. The value in the observation column 1.8 indicates the value, the value in the CENSORING column indicates that the value in the observation column is the upper bound. An additional column LIMIT reports the lower limit of the censored interval (0 in this example):
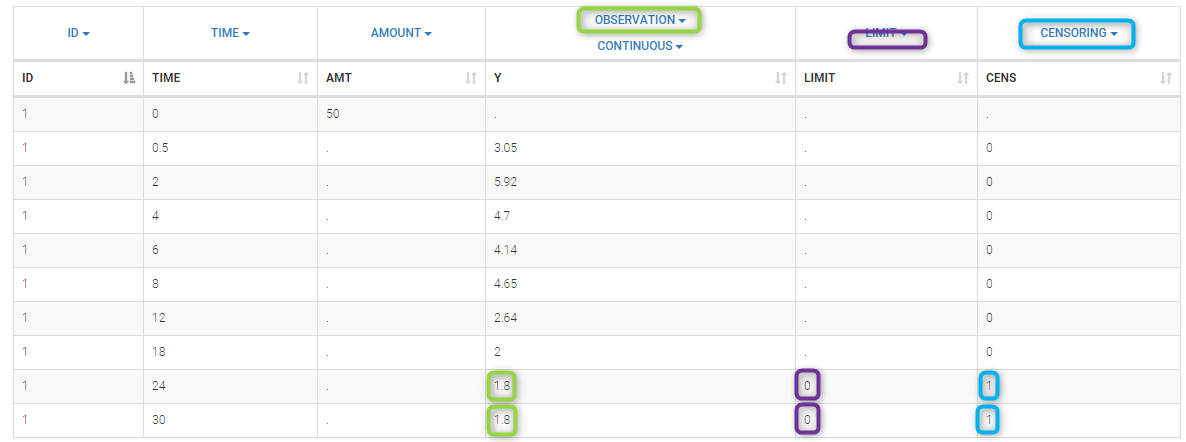
Remarks
- if this column is missing, then BLQ data is assumed to be left-censored data that can take any positive and negative value below LLOQ.
- the value of the limit can vary between observations of the same subject.
Monolix will use this additional information to estimate the model parameters properly and to impute the BLQ data for the diagnosis plots.
Plot of individual fits now displays LLOD at 1.8 with a red band when a PK data is censored. We see that the band lower limit is at 0 as defined in the limit column.
PK data below a lower limit of quantification or below a limit of detection
- censoring2_project (data = ‘censored2_data.txt’, model = ‘lib:oral1_1cpt_kaVk.txt’)
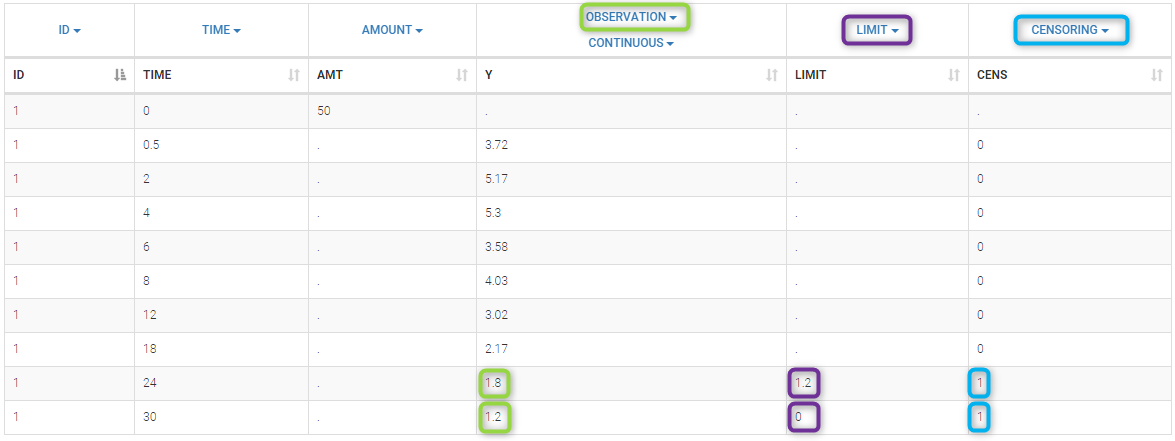 Plot of individual fits now displays LLOQ or LLOD with a red band when a PK data is censored. We see that the band lower limits depend on the observation.
Plot of individual fits now displays LLOQ or LLOD with a red band when a PK data is censored. We see that the band lower limits depend on the observation.
PK data below a lower limit of quantification and PD data above an upper limit of quantification
- censoring3_project (data = ‘censored3_data.txt’, model = ‘pkpd_model.txt’)
We work with PK and PD data in this project and assume that the PD data may be right censored and that the upper limit of quantification is ULOQ=90. We use CENS=-1 to indicate that an observation is right censored. In such case, the PD data can take any value above the upper limit reported in column Y (here the YTYPE column of type OBSERVED ID defines the type of observation, YTYPE=1 and YTYPE=2 are used respectively for PK and PD data):
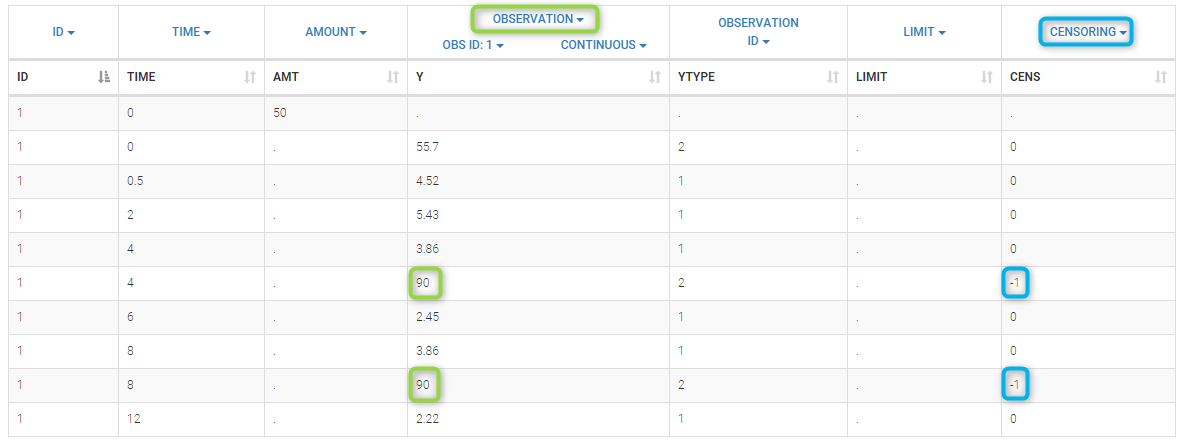 Plot of individual fits for the PD data now displays ULOQ and the predicted PD profile:
Plot of individual fits for the PD data now displays ULOQ and the predicted PD profile:
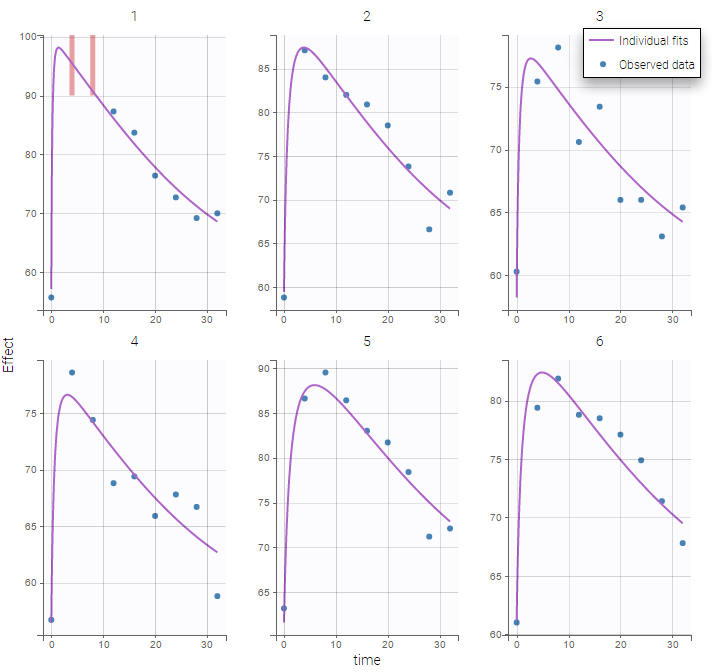
We can display the cumulative fraction of censored data both for the PK and the PD data (on the left and right respectively):
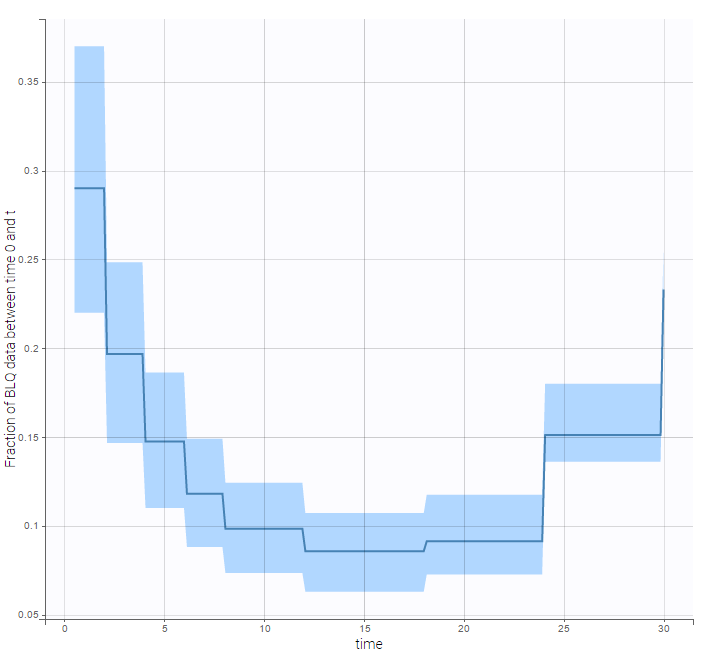 |
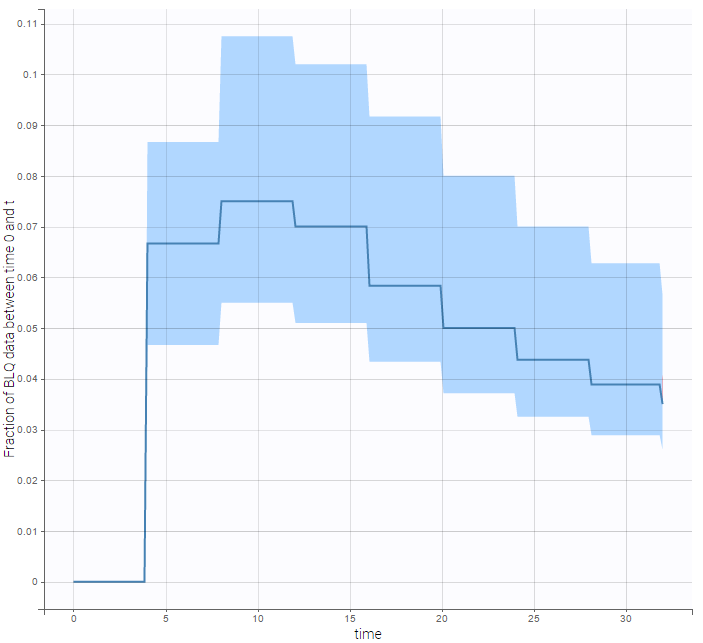 |
|---|
Combination of interval censored PK and PD data
- censoring4_project (data = ‘censored4_data.txt’, model = ‘pkpd_model.txt’)
We assume in this example
- 2 different censoring intervals(0,1) and (1.2, 1.8) for the PK,
- a censoring interval (80,90) and right censoring (>90) for the PD.
Combining columns CENS, LIMIT and Y allow us to combine efficiently these different censoring processes:
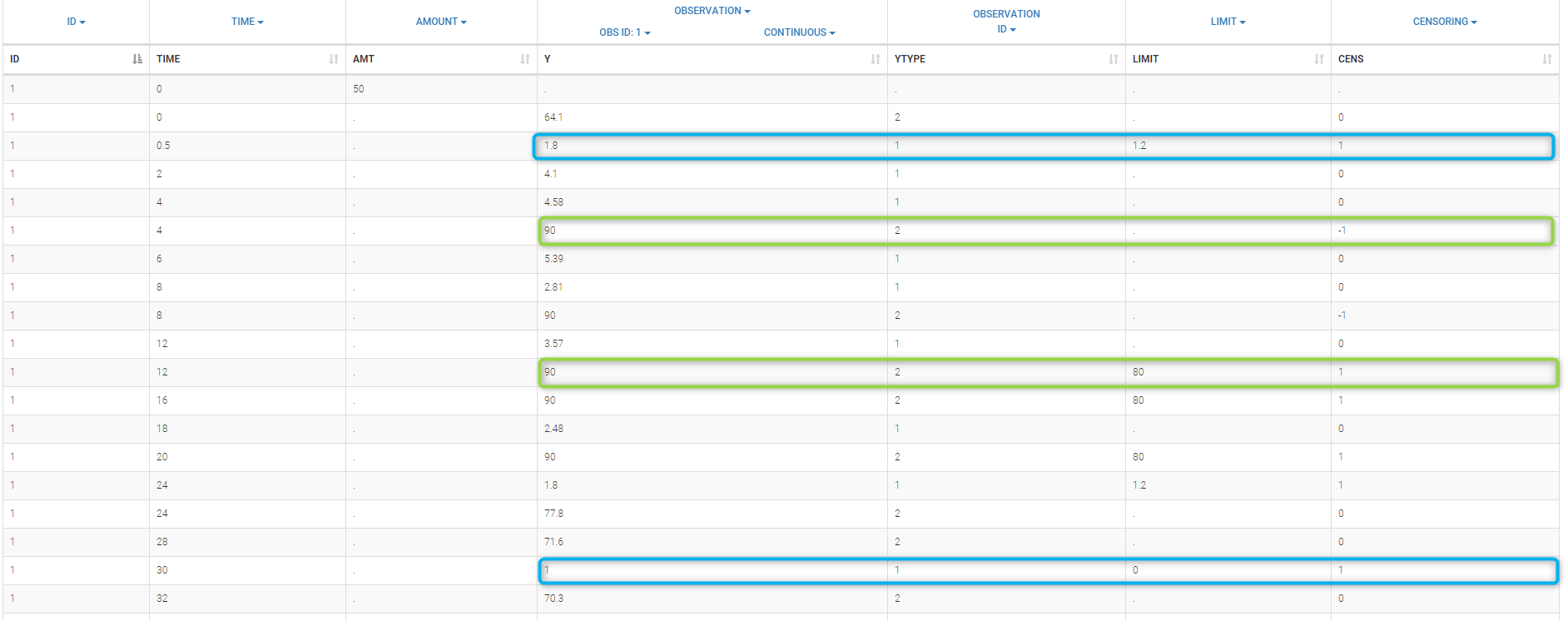
This coding of the data means that, for subject 1,
- PK data is between 0 and 1 at time 30h (second blue frame),
- PK data is between 1.2 and 1.8 at times 0.5h and 24h (first blue frame for time .5h),
- PD data is between 80 and 90 at times 12h and 16h (second green frame for time 12h),
- PD data is above 90 at times 4h and 8h (first green frame for time 4h).
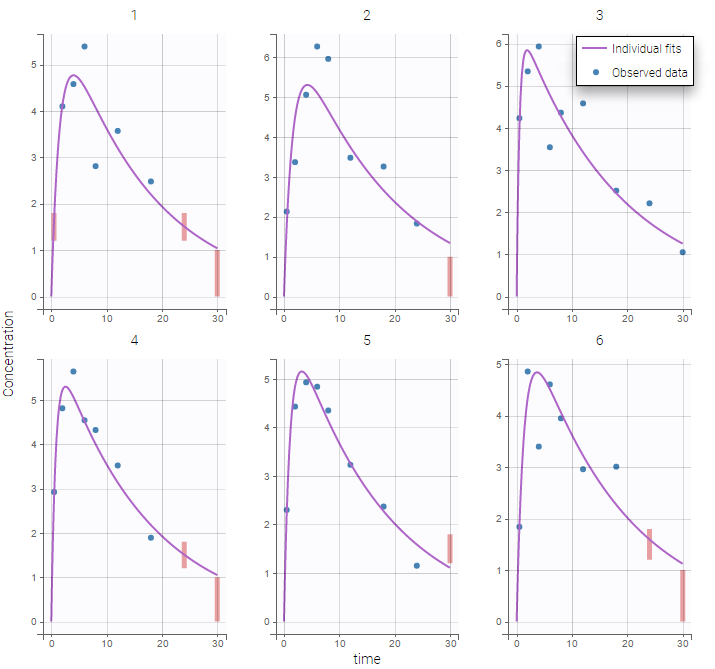
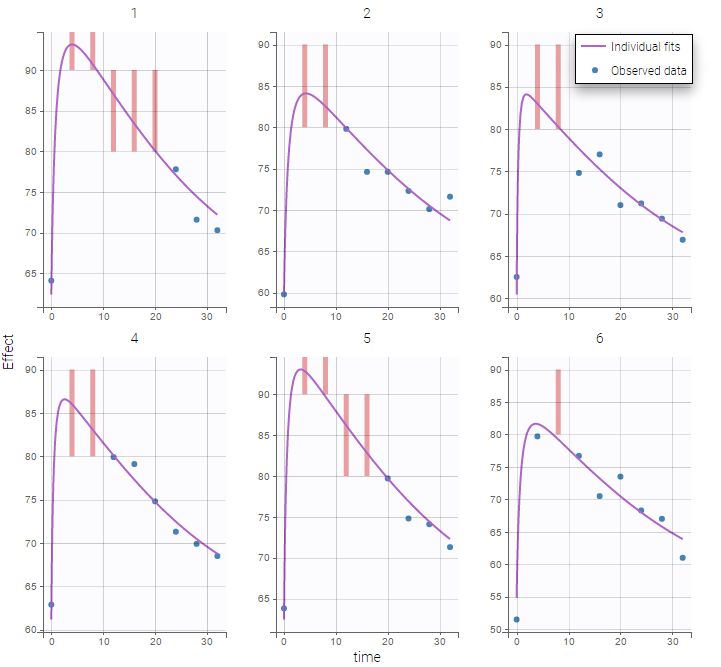
Plot of individual fits for the PK and the PD data displays the different limits of these censoring intervals (PK on the left and PD on the right):
 |
 |
|---|
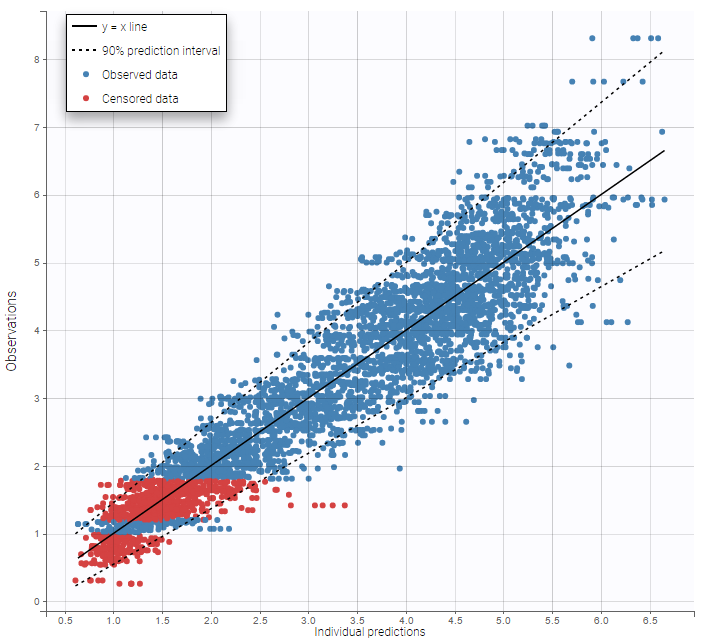
Other diagnosis plots, such as the plot of observations versus predictions, adequately use imputed censored PK and PD data:
 |
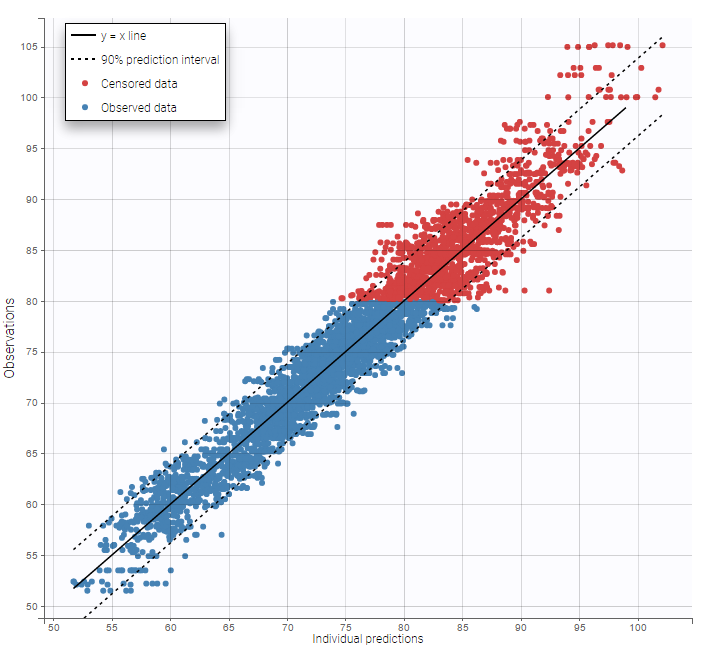 |
|---|
Case studies
- 8.case_studies/hiv_project (data = ‘hiv_data.txt’, model = ‘hivLatent_model.txt’)
- 8.case_studies/hcv_project (data = ‘hcv_data.txt’, model = ‘hcvNeumann98_model_latent.txt’)