When you launch the estimation of the population parameters, you can see the evolution of the population parameter estimates over the iterations of the SAEM algorithm but also the convergence indicator in purple.
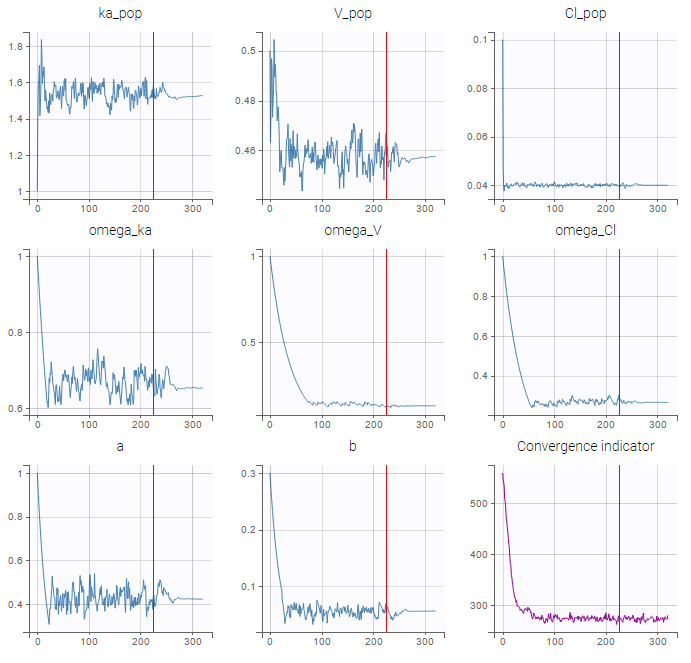
The convergence indicator is the complete log-likelihood. It can help to follow convergence.
Note that the complete likelihood is not the same as the log-likelihood computed as separate task.
Log-likelihood
The likelihood is the probability density of the data given the population parameter, so the log-likelihood is defined as:
\(\sum_{i=1}^{N_{\text{ind}}}\log\left(p(y_i; \theta)\right)\)
The likelihood is the objective function, therefore it is the relevant quantity to compare model, but unfortunately it cannot be computed in closed form because the individual parameters \(\phi_i\) are unobserved. It requires to integrate over all possible values of the individual parameters. Thus, to estimate the log-likelihood an importance sampling Monte Carlo method is used in a separate task (or an approximation is calculated via linearization of the model).
Complete log-likelihood
On the contrary, the complete likelihood refers to the joint probability distribution of the data and the individual parameters. The convergence indicator (complete log-likelihood) is then defined as:
\(\sum_{i=1}^{N_{\text{ind}}}\log\left(p(y_i, \phi_i; \theta)\right)\)
The joint probability distribution can be decomposed using Bayes law as:
\(p(y_i, \psi_i; \theta)=p(y_i| \psi_i; \theta)p(\psi_i; \theta)\)
Those two terms have an analytical expression and are easy to calculate, using as \(\phi_i\) the individual parameters drawn by MCMC for the current iteration of SAEM. This quantity is calculated at each SAEM step and is useful to assess the convergence of the SAEM algorithm.
Typical shape of the convergence indicator
Typically, the convergence indicator decreases progressively and then stabilizes. The convergence indicator aggregates the information from all parameters and can serve to detect if the SAEM algorithm has already converged or not. When the indicator is stable, that is it oscillates around the same value without drifting, then we can be pretty confident that the maximum likelihood has been achieved.