Introduction to time-to-event modeling with the MonolixSuite

Within the MonolixSuite, the mlxtran language allows to describe and model time-to-event data. In Part 1 of this case study, we give an introduction on time-to-event data, the different ways to model this kind of data, and typical parametric models.

What is time-to-event data

In case of time-to-event data the recorded observations are the times at which events occur. We can for instance record the time (duration) from diagnosis of a disease until death, or the time between administration of a drug and the next epileptic seizures. In the first case, the event is one-off, while in the second it can be repeated.
In addition, the event can be:

exactly observed: we know the event has happen exactly at time $t_i$ $(T_i=t_i)$
interval censored: we know the event has happen during a time interval, but not exactly when $(a_i \leq T_i \leq b_i)$
right censored: the observation period ends before the event can be observed $(T_i > t_{end})$

Formatting of time-to-event data in the MonolixSuite

In the data set, exactly observed events, interval censored events and right censoring are recorded for each individual. Contrary to other softwares for survival analysis, the MonolixSuite requires to specify the time at which the observation period starts. This allow to define the data set using absolute times, in addition to durations (if the start time is zero, the records represent durations between the start time and the event).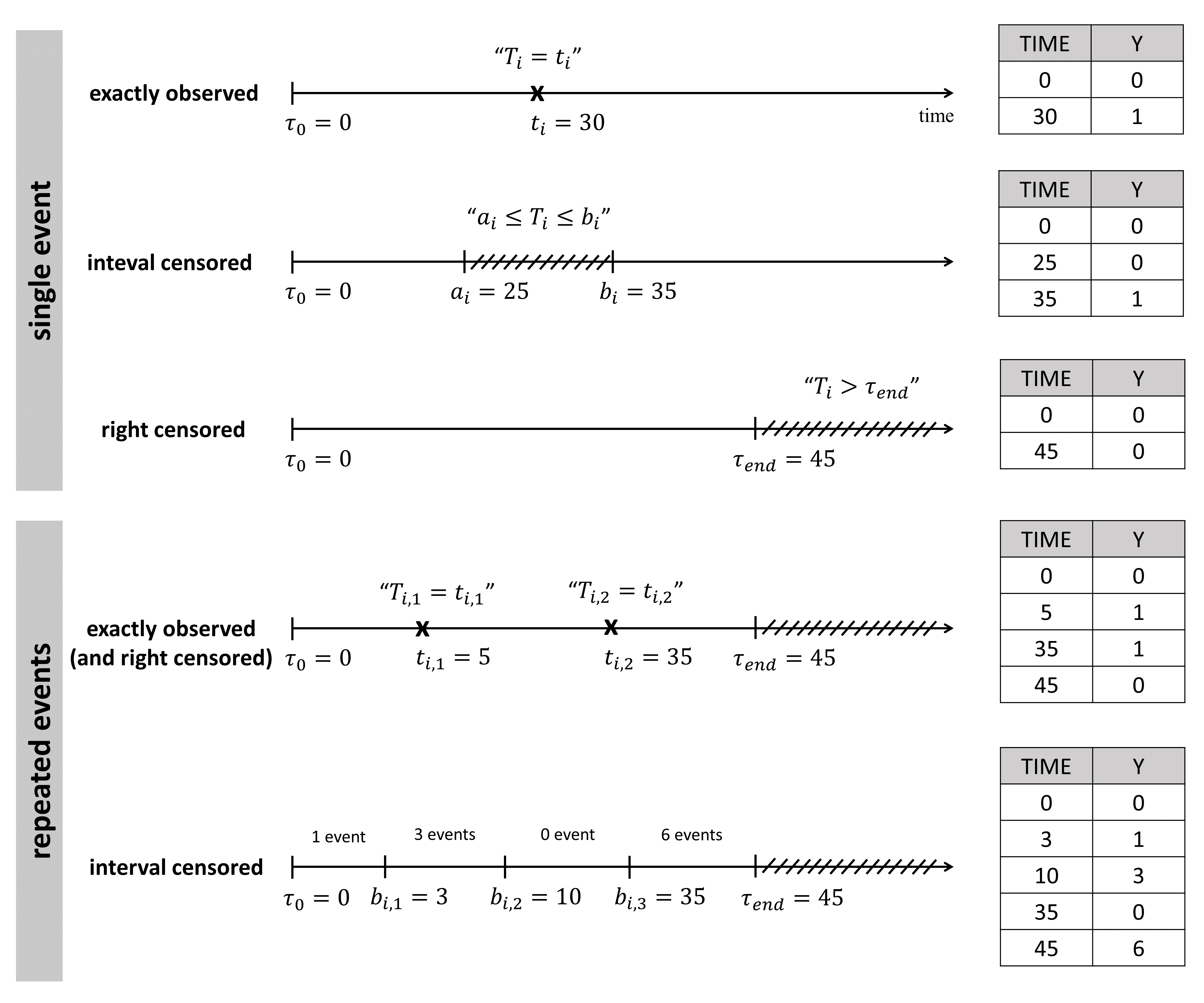

For instance for single events, exactly observed (with or without right censoring), one must indicate the start time of the observation period (Y=0), and the time of event (Y=1) or the time of the end of the observation period if no event has occurred (Y=0). In the following example:

the observation period last from starting time t=0 to the final time t=80. For individual 1, the event is observed at t=34, and for individual 2, no event is observed during the period. Thus it is indicated that at the final time (t=80), no event had occurred. Using absolute times instead of durations, we could equivalently write:

The durations between start time and event (or end of the observation period) are the same as before, but this time we record the day at which the patients enter the study and the days at which they have events or leave the study. Different patients may enter the study at different times.

Examples for repeated events, and interval censored events are available on the data set documentation page.

Important concepts: hazard and survival

Two functions have a key role in time-to-event analysis: the survival function and the hazard function. The survival function S(t) is the probability that the event happens after time t. A common way to estimate it non-parametrically is to calculate the Kaplan-Meier estimate. The hazard function h(t) is the instantaneous rate of an event, given that it has not already occurred. Both are linked by the following equation
$$S(t)=e^{-\int_0^t h(x) dx}$$

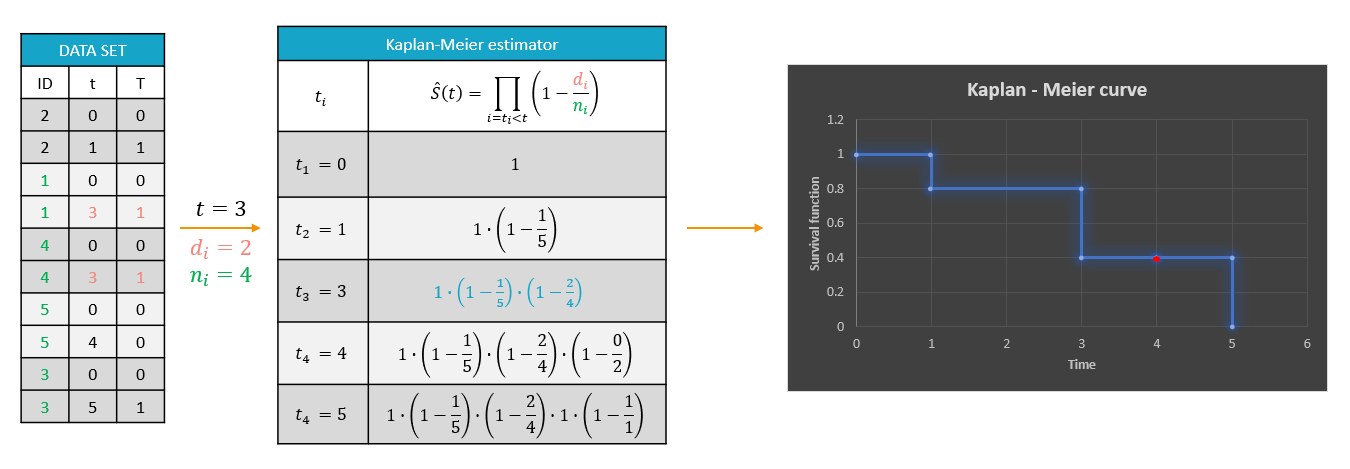
Kaplan-Meier estimator

The survival function S(t) is unknown and a typical way to approximate is the non-parametric Kaplan-Meier estimator. It describes the probability that an individual survives until time t, knowing that it survived at any earlier time and, for single events, is given by the following formula
$$\hat{S}(t)=\sum_{i:t_i<t} \left(1-\frac{d_i}{n_i}\right),$$
where

$t_i$ – times before t, when at least one event occurred,
$d_i$ – number of events at the time $t_i$,
$n_i$ – number of individuals at risk, that is who did not experience an event until $t_i$.

The probability that an event occurs $(p_e)$ is the ratio between the number of events that has occurred $(d_i)$ and the total number of individuals at risk $(n_i)$. The complement of it, $(1-p_e)$, gives an estimation of the survival. For each time t, the probabilities calculated at all previous times $t_i$, when at least one event occurred, have to be multiplied because the total number of individuals at risk changed. It is similar to calculating the probability that a patient survives 2 days. It is a product of a probability that a patient survives the first day and a conditional probability that it survives the second day, knowing that it survived the first one.

Example: A typical example of a time-to-event data set contains information about exact times when individuals experienced an event or when they left a study (drop-out). In the following, there are five individuals, who have two observations: time when the observation starts, which is 0 for all, and time of an event. If a patient leaves a study, then the time of a drop-out is given but instead of 1 in the column for the observation, there is 0. It indicates that this individual didn’t experience an event but survived until the drop-out time.The advantage of the Kaplan-Meier estimate is that it takes into account situations when not all individuals continue the study. At the next event time, such individuals are not counted as individuals at risk and are not counted in the denominator $n_i$.

A study starts at time $t_1$. There are no events, so $d_1=0$ and the value of the survival curve is 1. Until the next event time at $t_2=1$, the survival remains constant. Then, one individual experienced an event, so $d_2=1$, and all individuals survived until that time, so $n_2=5$. The result is that the probability to survive decreases by 0.2, which corresponds to the height of the jump at $t=1$ in the plot. Then again, until the next event, survival remains constant. At time $t=3$, there are two events. The number $n_3$ counts now only 4 individuals – it has decreased by 1 due to the previous event. To get the final value we have to multiply the current probability by all earlier probabilities. At $t=4$ there is a drop-out. Patient 5 left the study and no event was registered. The survival curve remains constant, and the drop-out is marked in red. The Kaplan-Meier estimator takes into account this situations, because at the next event time $t=5$, this individual is not counted as an individual at risk and is not counted in the denominator n. So at time $t=5$, there is only one individual left, and one event, so the survival equals 0.

Information about individuals who left the study is handled correctly. But the Kaplan-Meier estimator can be biased when the exact times of events are unknown and information only about the time intervals is available. For example, assume that an observation period started at $t=0$ and at $t=1$ an event is marked by 1 in the column for the observation. It is impossible to distinguish in the dataset, without any other information, if the event was exactly at $t=1$ or before. The same problem is when a time of the beginning of the study and time interval limits of an event are given. Just looking at the data set, an exact and interval censored event type are indistinguishable. This is why, for data visualization in Monolix, it is assumed that all events are exactly observed. That is, not knowing when an event happened, it is assumed that it happened at the end of the censored interval.

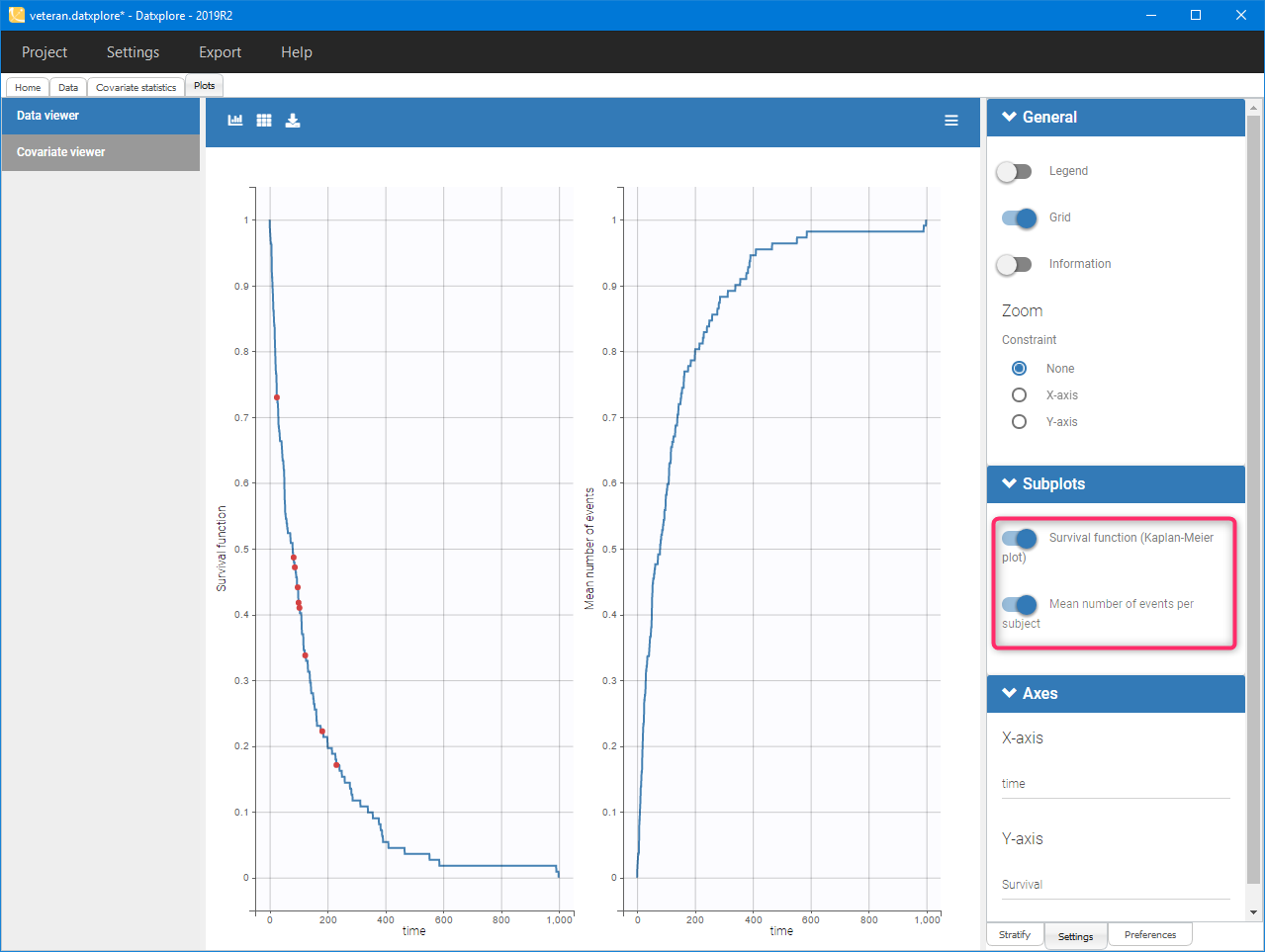
Mean number of events. The Kaplan-Meier estimator can be used also for the analysis of repeated events. The survival curve is estimated for each k-th event separately

$$\hat{S}^{(k)}(t)=\sum_{i:t_i<t} \left(1-\frac{d^{(k)}_i}{n^{(k)}_i}\right),$$

and is used to calculate the mean number of events per individual as a function of time

$$\hat{m}(t)=\sum_{k} \left(1-\hat{S}^{(k)}(t)\right).$$

It can be visualized in Datxplore and Monolix next to the Survival function by choosing this option from the Subplots settings:

Different types of approaches

Depending on the goal of the time-to-event analysis, different modeling approaches can be used: non-parametric, semi-parametric (Cox models) and parametric.

Non-parametric models do not require assumptions on the shape of the hazard or survival. Using the Kaplan-Meier estimate, statistical tests can be performed to check if the survival differs between sub-populations. The main limitations of this approach are that (i) only categorical covariates can be tested and (ii) the way the survival is affected by the covariate cannot be assessed.
Semi-parametric models (Cox models) assume that the hazard can be written as a baseline hazard (that depends only on time), multiplied by a term that depends only on the covariates (and not time). Under this hypothesis of proportional covariate effect, one can analyze the effect of covariates (categorical and continuous) in a parametric way, leaving the baseline hazard undefined.
Parametric models require to fully specify the hazard function. If a good model can be found, statistical tests are more powerful than for semi-parametric models. In addition, there is no restrictions on how the covariates affects the hazard. Parametric models can also be easily used for predictions.

The table below synthesizes the possibilities for the 3 approaches.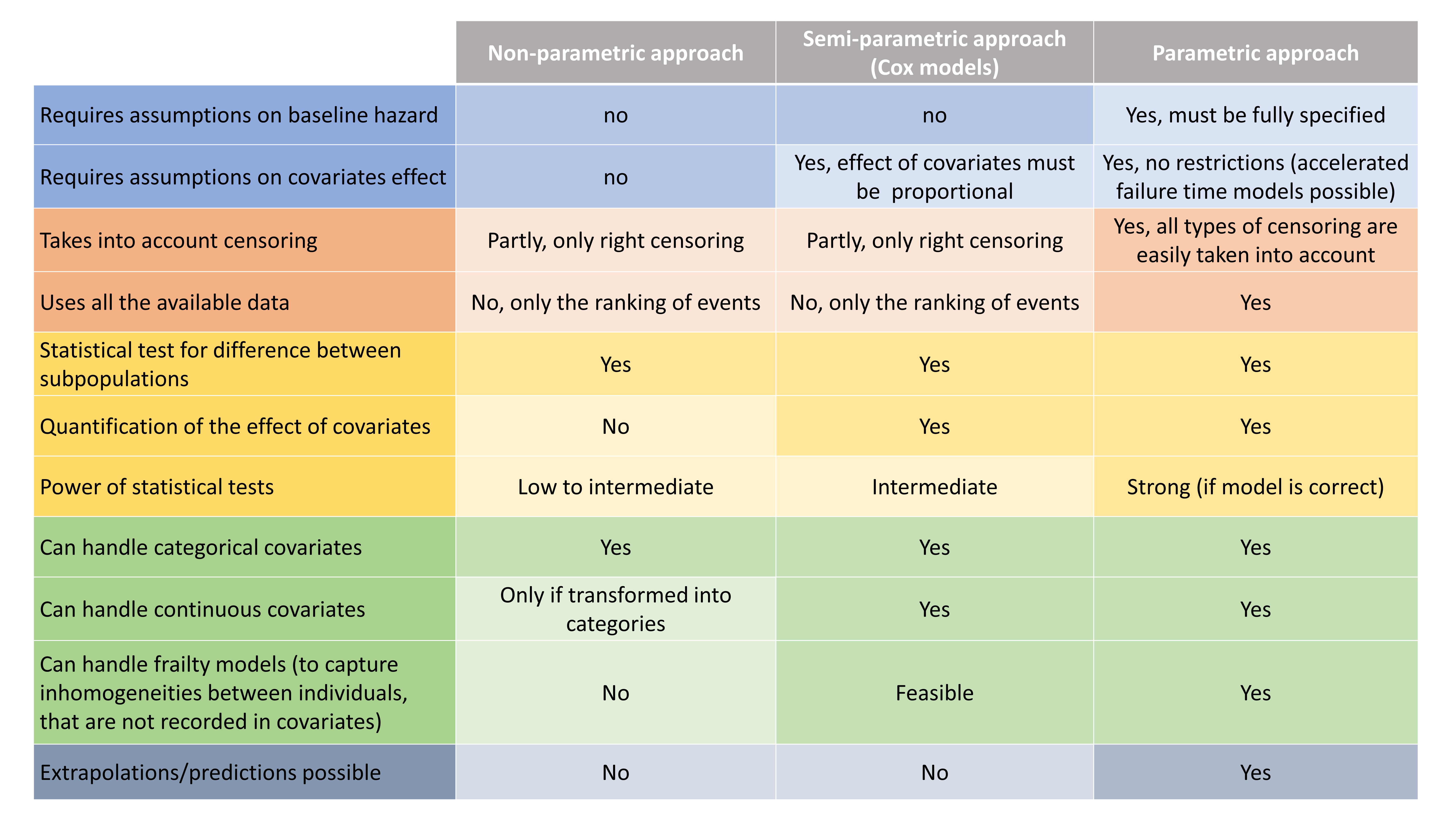

Focus on parametric modeling with the MonolixSuite

In the MonolixSuite, the only possible approach is the parametric approach. The model is defined via the hazard function, which in a population approach typically depends on individual parameters: $h(t,\psi_i)$. With the hazard function, the survival function can easily be computed, as well as the conditional distribution $p_{y_i|\psi_i}$ for various censoring situations (which is required for parameter estimation via SAEM, log-likelihood calculation, etc).

The typical syntax to define the output is the following:

DEFINITION:
Event = {type=event, maxEventNumber=1, hazard=h}

The output Event will be matched to the time-to-event data of the data set. The hazard function h is usually defined via an expression including the input individual parameters. For one-off events, the maximal number of events per individual is 1. It is important to indicate it in the maxEventNumber argument to speed up calculations. To use the model for simulations with Simulx, rightCensoringTime must be given as additional argument. Check here for details.

Note that the hazard can be a function of other variables such as drug concentration or tumor burden for instance (joint PK-TTE or PD-TTE models). An example of the syntax is given here.

Proportional hazard models and hazard ratios

Proportional hazard models are one subclass of models for time-to-event data. In a proportional hazard model, the hazard can be written as the product of a first term (baseline hazard) that depends only on time $t$ and some parameters $\theta$, and a second term (link function) that depends only on the covariates $cov$ and some parameters $\theta$. To ensure a positive hazard, the link is commonly the exponential function.

$$h(t,\theta,cov)=h_0(t,\theta) \times \exp(\beta \times cov)$$

Hazard ratios for different values of covariates then only depend on $\beta$ and the covariate, as the baseline hazard cancel out. Thank to this property, proportional hazard models are widely used in the semi-parametric Cox approach. But they can also be implemented using a parametric form in Monolix.

Except for the exponential model (constant hazard), adding covariates on the parameters of the library models (see below for the library) does not lead to a proportional hazard model. Thus, the most convenient approach is to introduce a dummy parameter in the hazard definition, which will carry the covariates.

For instance, the log-logistic model from the library can easily be modified to add the dummy parameter “h_cov”, both in the input list and in the hazard definition:

[LONGITUDINAL]
input = {Te, s, h_cov}

EQUATION:
h = s/Te * (t/Te)^(s-1) / (1+(t/Te)^s) * h_cov

DEFINITION:
Event = {type=event, maxEventNumber=1, hazard=h}

OUTPUT:
output = {Event}

The statistical model must then be defined in the following way:

remove the random effects on h_cov. Keep the default log-normal distribution.
fix the value of the fixed effect h_cov_pop to 1
add untransformed covariates on h_cov.

Using a log-normal distribution and untransformed covariates will lead to the following hazard. For the example, we assume that AGE and TRT have been added on h_cov.

$$h=\frac{\frac{s}{Te}\left(\frac{t}{Te}\right)^{s-1}}{1+\left(\frac{t}{Te}\right)^s}\times 1 \times \exp(\beta_{AGE}\times AGE) \times \exp(\beta_{TRT} [\textrm{if } TRT=1])$$

The estimated betas and their standard errors are displayed in the Monolix results. Note that the Wald test is also given and that automatic covariate search strategies can be applied.

This strategy with the dummy parameter does not allow to consider interaction between covariates. If this is needed, the covariates can be passed as regressor and the covariate model can be implemented directly in the structural model.

Library of parametric models for time-to-event data

To describe the various shapes that the survival Kaplan-Meier estimate can take, several hazard functions have been proposed. Below we display the survival curves, for the most typical hazard functions:

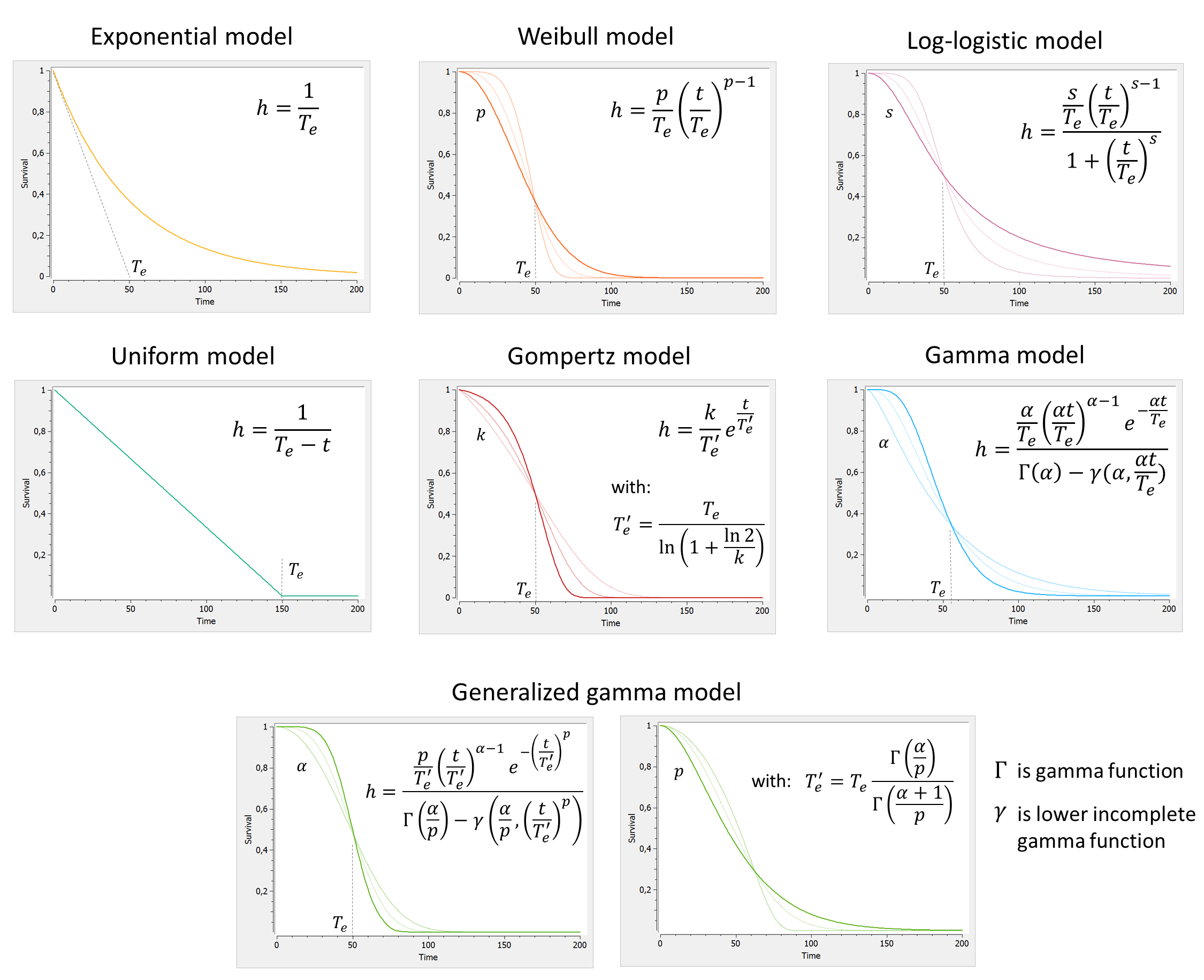
A few comments:

We have reparametrized $ T_e’ $ as a function of $ T_e $ to better separate the effects of the scale parameter (characteristic time) and the shape parameter (shape of the curve).
All parameters are positive. If we assume inter-individual variability, a log-normal distribution is usually appropriate.

The table below summarizes the number of parameters and typical parameter values: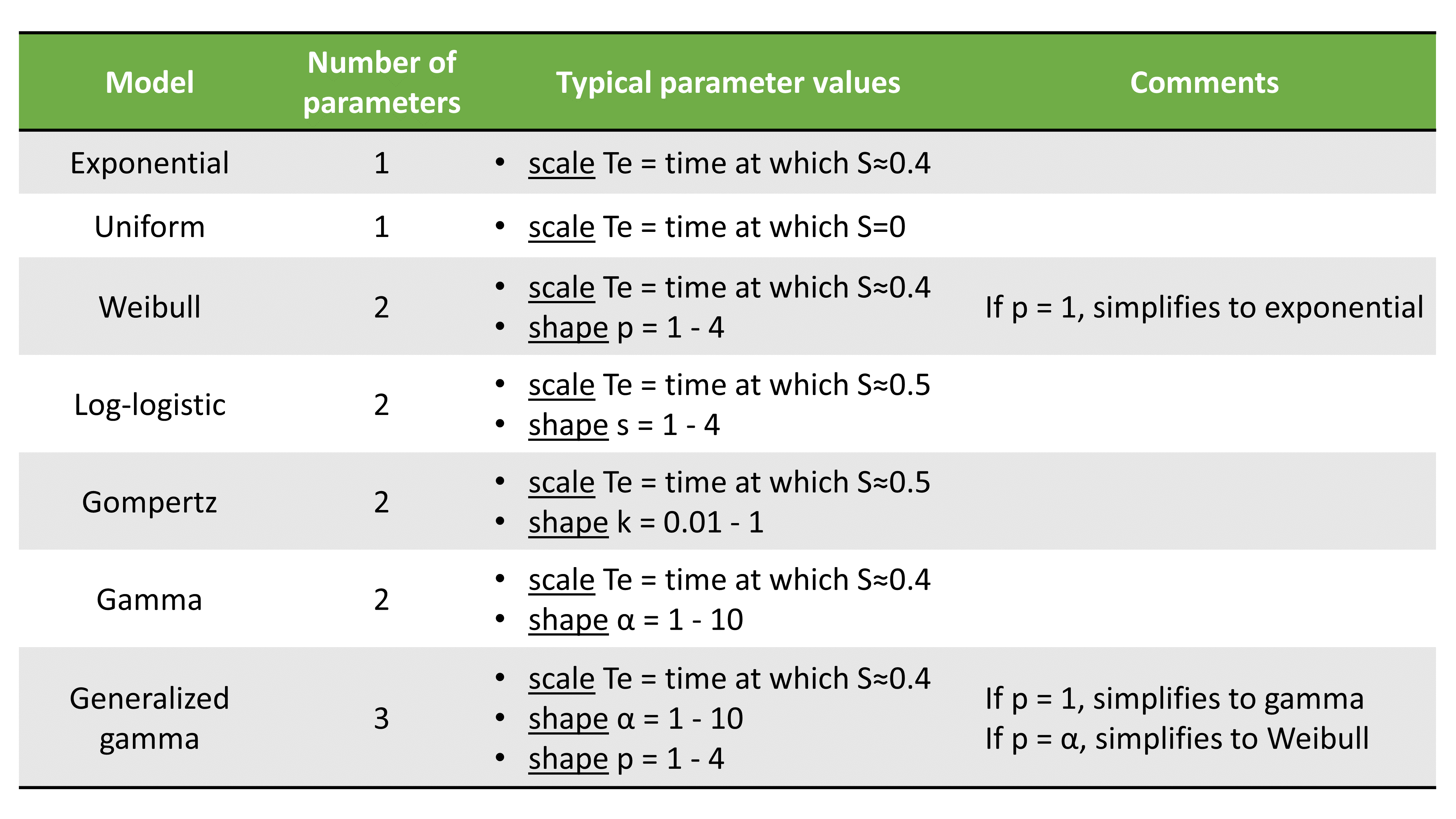

For each model, we can in addition consider a delay del as additional parameter. The delay will simply shift the survival curve to the right (later times). For t<del, the survival is S(t<del)=1.

Downloads:

All models are available as Mlxtran model file in the TTE library. Each model can be with/without delay and for single/repeated events. For performance reasons, it is important to choose the file ending with ‘_singleEvent.txt’ if you want to model one-off events (death, drop-out, etc).

Case studies

Two case studies show the modeling and simulation workflow for TTE data:

Time-to-event modeling with the MonolixSuite, Part 1: Introduction