- Introduction
- Formatting of categorical data in the MonolixSuite
- Ordered categorical data
- Ordered categorical data with regression variables
- Discrete-time Markov chain
- Continuous-time Markov chain
Objectives: learn how to implement a model for categorical data, assuming either independence or a Markovian dependence between observations.
Projects: categorical1_project, categorical2_project, markov0_project, markov1a_project, markov1b_project, markov1c_project, markov2_project, markov3a_project, markov3b_project
Introduction
Assume now that the observed data takes its values in a fixed and finite set of nominal categories \(\{c_1, c_2,\ldots , c_K\}\). Considering the observations \((y_{ij},\, 1 \leq j \leq n_i)\) for any individual \(i\) as a sequence of conditionally independent random variables, the model is completely defined by the probability mass functions \(\mathbb{P}(y_{ij}=c_k | \psi_i)\) for \(k=1,\ldots, K\) and \(1 \leq j \leq n_i\). For a given (i,j), the sum of the K probabilities is 1, so in fact only K-1 of them need to be defined. In the most general way possible, any model can be considered so long as it defines a probability distribution, i.e., for each k, \(\mathbb{P}(y_{ij}=c_k | \psi_i) \in [0,1]\), and \(\sum_{k=1}^{K} \mathbb{P}(y_{ij}=c_k | \psi_i) =1\). Ordinal data further assumed that the categories are ordered, i.e., there exists an order \(\prec\) such that
$$c_1 \prec c_2,\prec \ldots \prec c_K $$
We can think, for instance, of levels of pain (low \(\prec\) moderate \(\prec\) severe) or scores on a discrete scale, e.g., from 1 to 10. Instead of defining the probabilities of each category, it may be convenient to define the cumulative probabilities \(\mathbb{P}(y_{ij} \preceq c_k | \psi_i)\) for \(k=1,\ldots ,K-1\), or in the other direction: \(\mathbb{P}(y_{ij} \succeq c_k | \psi_i)\) for \(k=2,\ldots, K\). Any model is possible as long as it defines a probability distribution, i.e., it satisfies
$$0 \leq \mathbb{P}(y_{ij} \preceq c_1 | \psi_i) \leq \mathbb{P}(y_{ij} \preceq c_2 | \psi_i)\leq \ldots \leq \mathbb{P}(y_{ij} \preceq c_K | \psi_i) =1 .$$
It is possible to introduce dependence between observations from the same individual by assuming that \((y_{ij},\,j=1,2,\ldots,n_i)\) forms a Markov chain. For instance, a Markov chain with memory 1 assumes that all that is required from the past to determine the distribution of \(y_{ij}\) is the value of the previous observation \(y_{i,j-1}\)., i.e., for all \(k=1,2,\ldots ,K\),
$$\mathbb{P}(y_{ij} = c_k\,|\,y_{i,j-1}, y_{i,j-2}, y_{i,j-3},\ldots,\psi_i) = \mathbb{P}(y_{ij} = c_k | y_{i,j-1},\psi_i)$$
Formatting of categorical data in the MonolixSuite
In case of categorical data, the observations at each time point can only take values in a fixed and finite set of nominal categories. In the data set, the output categories must be coded as integers, as in the following example:
ID TIME Y 1 0.5 3 1 1 0 1 1.5 2 1 2 2 1 2.5 3
One can see the respiratory status data set and the warfarin data set for example for more practical examples on a categorical and a joint continuous and categorical data set respectively.
Ordered categorical data
- categorical1_project (data = ‘categorical1_data.txt’, model = ‘categorical1_model.txt’)
In this example, observations are ordinal data that take their values in {0, 1, 2, 3}:
- Cumulative odds ratio are used in this example to define the model
$$\textrm{logit}(\mathbb{P}(y_{ij} \leq k))= \log \left( \frac{\mathbb{P}(y_{ij} \leq k)}{1 – \mathbb{P}(y_{ij} \leq k )} \right)$$
where
$$\begin{array}{ccl} \text{logit}(\mathbb{P}(y_{ij} \leq 0)) &=& \theta_{i,1}\\ \text{logit}(\mathbb{P}(y_{ij} \leq 1)) &=& \theta_{i,1}+\theta_{i,2}\\ \text{logit}(\mathbb{P}(y_{ij} \leq 2)) &=& \theta_{i,1}+\theta_{i,2}+\theta_{i,3}\end{array}$$
This model is implemented in categorical1_model.txt:
[LONGITUDINAL]
input = {th1, th2, th3}
DEFINITION:
level = { type = categorical, categories = {0, 1, 2, 3},
logit(P(level<=0)) = th1
logit(P(level<=1)) = th1 + th2
logit(P(level<=2)) = th1 + th2 + th3
}
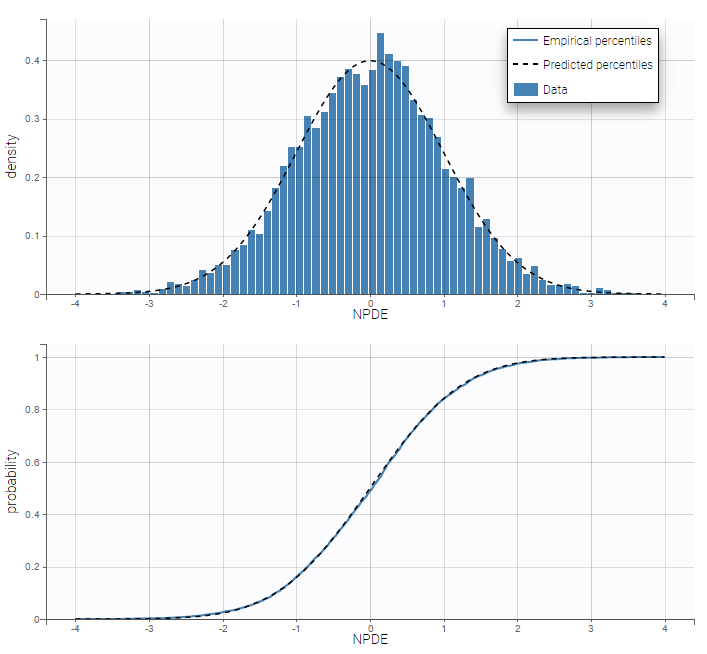
A normal distribution is used for \(\theta_{1}\), while log-normal distributions for \(\theta_{2}\) and \(\theta_{3}\) ensure that these parameters are positive (even without variability). Residuals for noncontinuous data reduce to NPDE’s. We can compare the empirical distribution of the NPDE’s with the distribution of a standardized normal distribution:
VPC’s for categorical data compare the observed and predicted frequencies of each category over time:
The prediction distribution can also be computed by Monte-Carlo:

Ordered categorical data with regression variables
- categorical2_project (data = ‘categorical2_data.txt’, model = ‘categorical2_model.txt’)
A proportional odds model is used in this example, where PERIOD and DOSE are used as regression variables (i.e. time-varying covariates)
Discrete-time Markov chain
If observation times are regularly spaced (constant length of time between successive observations), we can consider the observations \((y_{ij},j=1,2,\ldots,n_i)\) to be a discrete-time Markov chain.
- markov0_project (data = ‘markov1a_data.txt’, model = ‘markov0_model.txt’)
In this project, states are assumed to be independent and identically distributed:
\( \mathbb{P}(y_{ij} = 1) = 1 – \mathbb{P}(y_{ij} = 2) = p_{i,1} \)
Observations in markov1a_data.txt take their values in {1, 2}.
- markov1a_project (data = ‘markov1a_data.txt’, model = ‘markov1a_model.txt’)
Here,
\(\begin{aligned}\mathbb{P}(y_{i,j} = 1 | y_{i,j-1} = 1) = 1 – \mathbb{P}(y_{i,j} = 2 | y_{i,j-1} = 1) = p_{i,11}\\ \mathbb{P}(y_{i,j} = 1 | y_{i,j-1} = 2) = 1 – \mathbb{P}(y_{i,j} = 2 | y_{i,j-1} = 2) = p_{i,12} \end{aligned}\)
[LONGITUDINAL]
input = {p11, p21}
DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
P(State=1|State_p=1) = p11
P(State=1|State_p=2) = p21
}
The distribution of the initial state is not defined in the model, which means that, by default,
\( \mathbb{P}(y_{i,1} = 1) = \mathbb{P}(y_{i,1} = 2) = 0.5 \)
- markov1b_project (data = ‘markov1b_data.txt’, model = ‘markov1b_model.txt’)
The distribution of the initial state, \(p = \mathbb{P}(y_{i,1} = 1)\), is estimated in this example
DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
P(State_1=1)= p
P(State=1|State_p=1) = p11
P(State=1|State_p=2) = p21
}
- markov3a_project (data = ‘markov3a_data.txt’, model = ‘markov3a_model.txt’)
Transition probabilities change with time in this example. We then define time varying transition probabilities in the model:
[LONGITUDINAL]
input = {a1, b1, a2, b2}
EQUATION:
lp11 = a1 + b1*t/100
lp21 = a2 + b2*t/100
DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
logit(P(State=1|State_p=1)) = lp11
logit(P(State=1|State_p=2)) = lp21
}
- markov2_project (data = ‘markov2_data.txt’, model = ‘markov2_model.txt’)
Observations in markov2_data.txt take their values in {1, 2, 3}. Then, 6 transition probabilities need to be defined in the model.
Continuous-time Markov chain
The previous situation can be extended to the case where time intervals between observations are irregular by modeling the sequence of states as a continuous-time Markov process. The difference is that rather than transitioning to a new (possibly the same) state at each time step, the system remains in the current state for some random amount of time before transitioning. This process is now characterized by transition rates instead of transition probabilities:
\( \mathbb{P}(y_{i}(t+h) = k,|,y_{i}(t)=\ell , \psi_i) = h \rho_{\ell k}(t,\psi_i) + o(h),\qquad k \neq \ell .\)
The probability that no transition happens between \(t\) and \(t+h\) is
\( \mathbb{P}(y_{i}(s) = \ell, \forall s\in(t, t+h) | y_{i}(t)=\ell , \psi_i) = e^{h , \rho_{\ell \ell}(t,\psi_i)} .\)
Furthermore, for any individual i and time t, the transition rates \((\rho_{\ell,k}(t, \psi_i))\) satisfy for any \(1\leq \ell \leq K\),
\( \sum_{k=1}^K \rho_{\ell k}(t, \psi_i) = 0\)
Constructing a model therefore means defining parametric functions of time \((\rho_{\ell,k})\) that satisfy this condition.
- markov1c_project (data = ‘markov1c_data.txt’, model = ‘markov1c_model.txt’)
Observation times are irregular in this example. Then, a continuous time Markov chain should be used in order to take into account the Markovian dependence of the data:
DEFINITION:
State = { type = categorical, categories = {1,2}, dependence = Markov
transitionRate(1,2) = q12
transitionRate(2,1) = q21
}
- markov3b_project (data = ‘markov3b_data.txt’, model = ‘markov3b_model.txt’)
Time varying transition rates are used in this example.