Starting from the 2019 version, the section Proposal in the tab Results includes automatic proposals of improvements for the statistical model, based on comparisons of many correlation, covariate and error models.
Model selections are performed by using a BIC criteria (called Criteria in the interface), based on the current simulated individual parameters. This is why the proposal is computed by the task Conditional distribution.
Note that the BIC criteria is not the same as the BIC computed for the Monolix project with the task log-likelihood: it does not characterize the whole model but only each part of the statistical model evaluated in the proposal, and thus yields different values for each type of model. Each criteria is given by the formula:
\(BIC = -2\log({\cal L’})/nRep+\log(N) * k\),
where:
- \(\cal L’\) = likelihood of the linear regression
- N = number of individuals
- k = number of estimates betas
- nRep = number of replicates (samples per individual)
The number of estimated parameters k characterizes the part of the statistical model that is evaluated. The likelihood \(\cal L’\) is not the same as the one computed by the log-likelihood task, it is based on the joint distribution:
\(p(y_i, \phi_i; \theta)=p(y_i| \phi_i; \theta)p(\phi_i; \theta)\)
where all the parameters are fixed to the values estimated by Monolix except the parameters characterizing the model that is evaluated: error parameters (in \(\theta\)) for the error models, individual parameters or random effects (in \(\phi_i\)) for the covariate models or the correlation models.
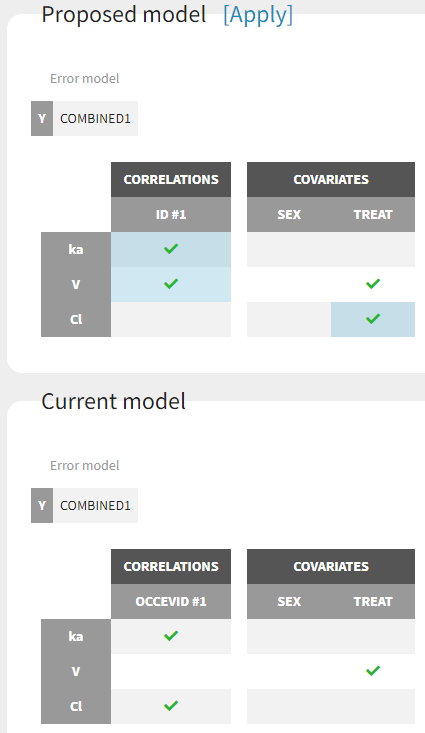
Proposed model
The section Proposal is organized in 4 tabs. The first tab summarizes the best proposal for the statistical model, that is the combination of best proposals for the error, covariate and correlation models.
The current statistical model is displayed below the proposed model, and the differences are highlighted in light blue.
The proposed model can be applied automatically with the button “Apply”. This modifies the current project to include all elements of the proposed statistical model. It is then recommended to save the project under a new name to avoid overwriting previous results.
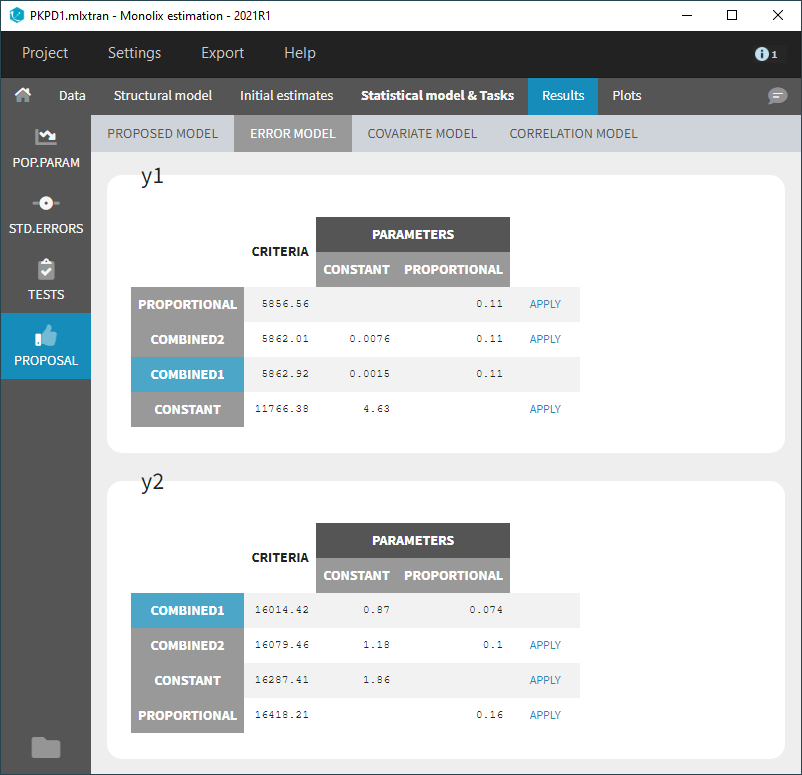
Error model
The error model selection is done by computing the criterion for each possible residual error model (constant, proportional, combined1, combined2), where the error parameters are optimized based on the data and the current predictions, for each observation model.
The evaluated models are displayed for each observation mode in increasing order of criterion. The current error model is highlighted in blue.
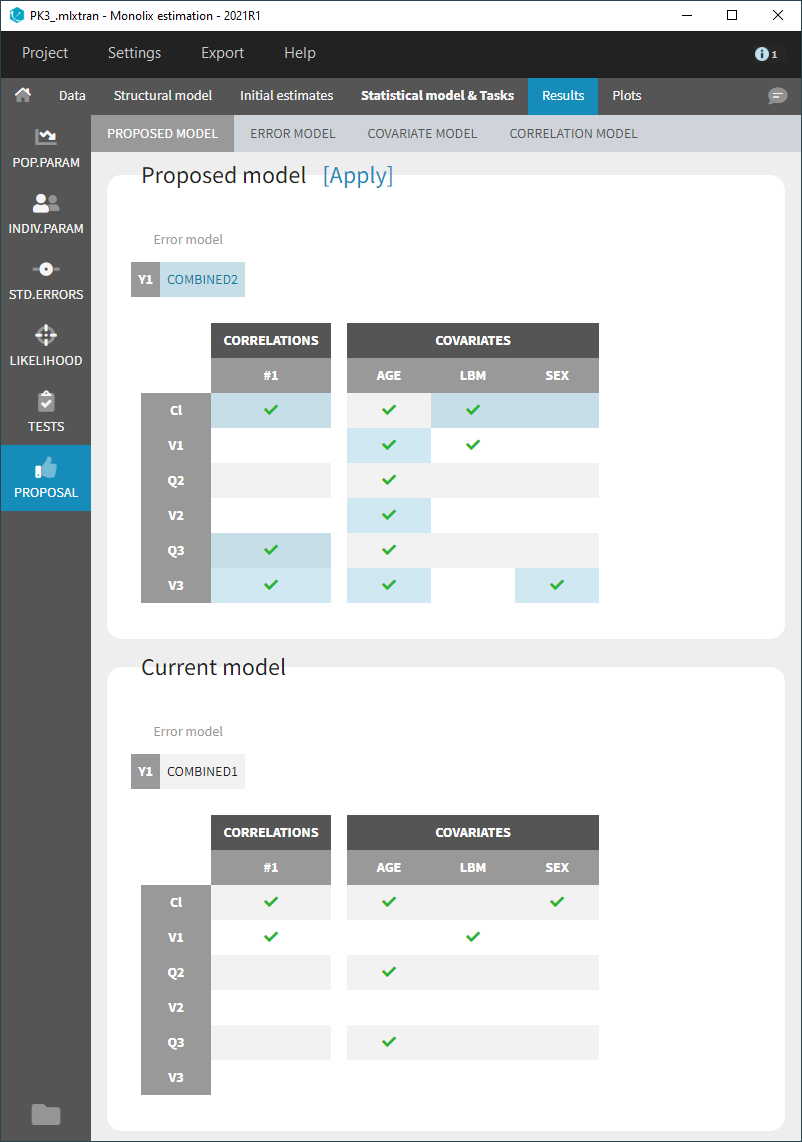
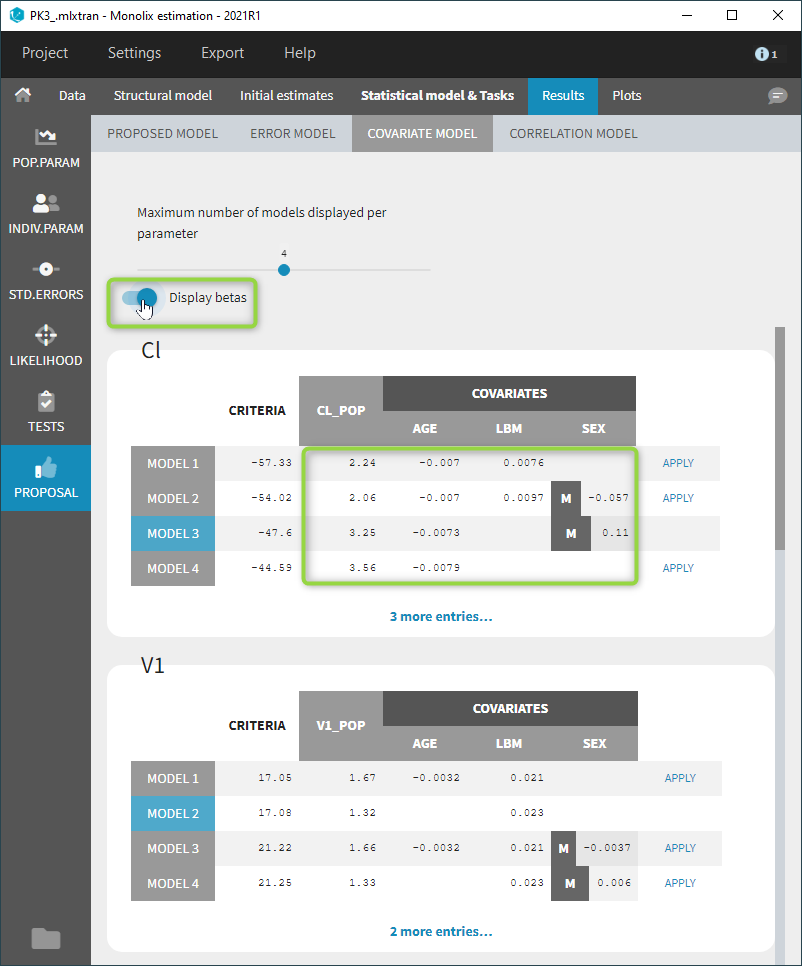
Covariate model
The covariate model selection is based on the evaluation of the criterion for each individual parameter independently.
For each individual parameter, all covariate models obtained by adding or removing one covariate are evaluated: beta parameters are estimated with linear regression, and the criterion is computed. The model with the best criterion is retained to continue the same procedure.
All evaluated models are displayed for each parameter, in increasing order of criterion. The current covariate model is highlighted in blue.
Since possibly many covariate models can be evaluated for each parameter, the maximum number of displayed models per parameter is 4 by default and can be changed with a slider, as below. Additional evaluated models can still be displayed by clicking on “more entries” below each table.
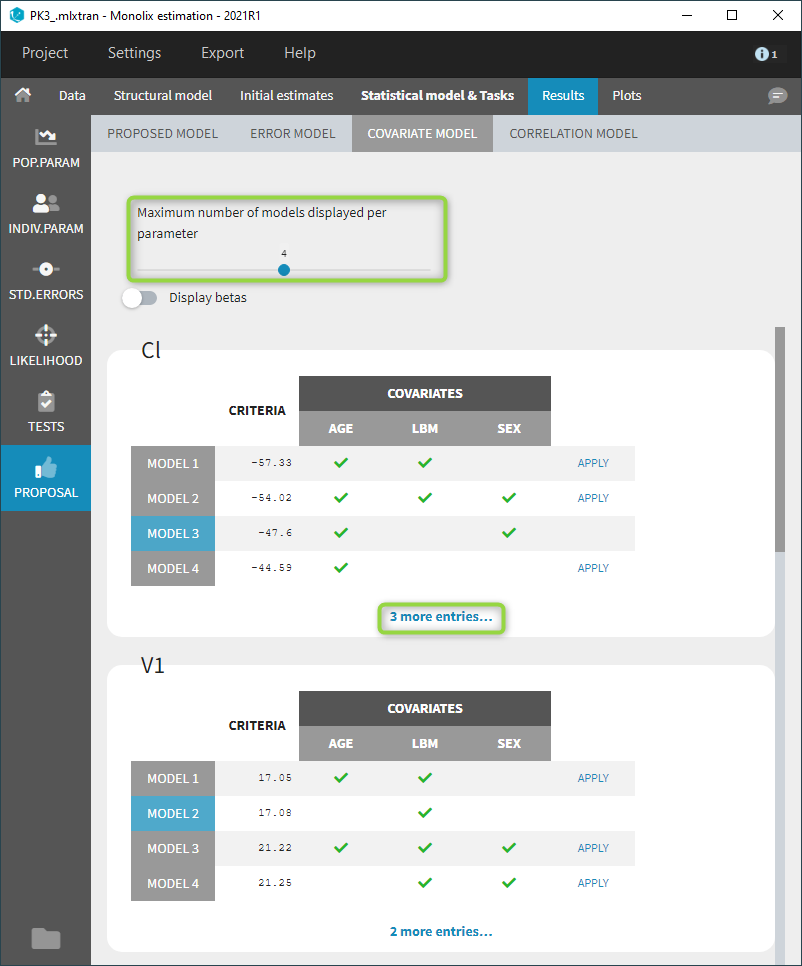
Beta parameters are computed for each evaluated model by linear regression. They are not displayed by default, but can be displayed with a toggle as shown below. For categorical covariates, the categories corresponding to the beta parameters are also displayed.
Correlation model
The correlation model selection is done by computing the criterion for each possible correlation block at each dimension, starting with the best solution from the previous dimension. The correlation models are displayed by increasing value of criterion. The current correlation model is highlighted in blue.
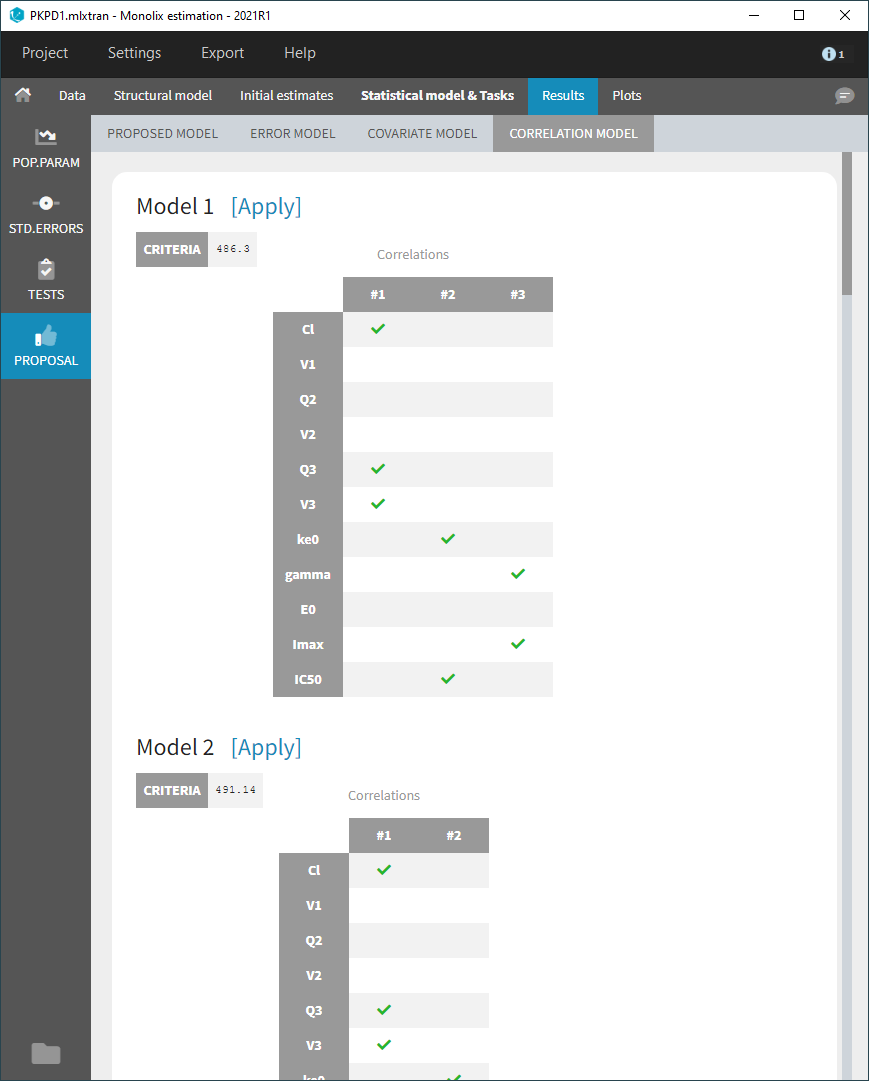
In Monolix2021, the correlation model includes also random effects at the inter-occasion level, like in the example below, while they were excluded from the proposal in previous versions.