Purpose
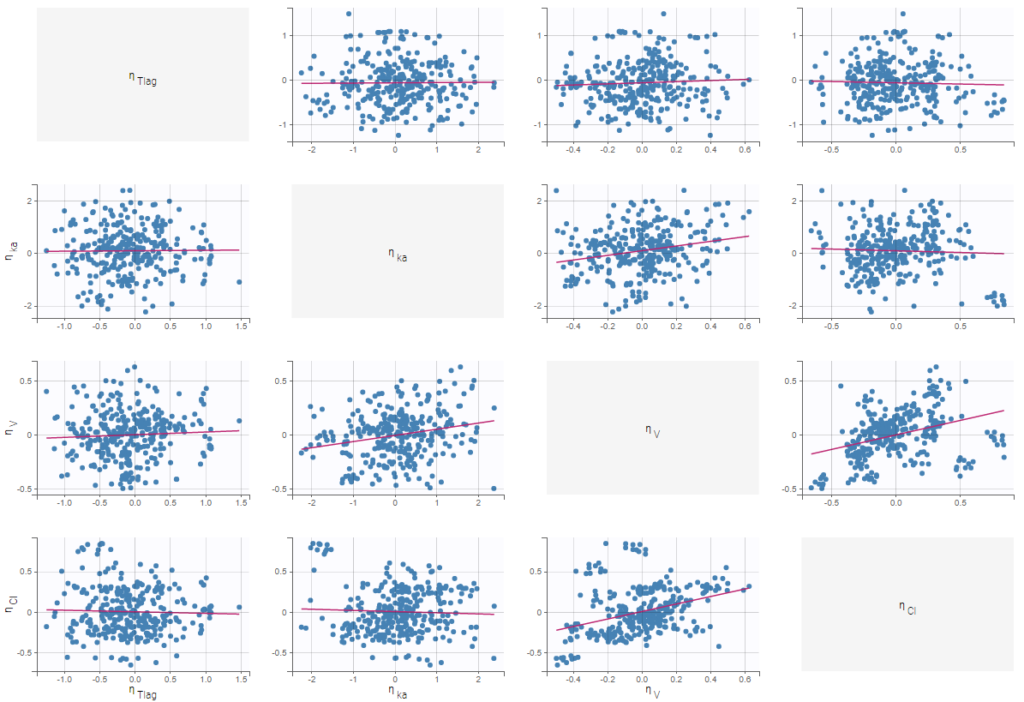
This plot displays scatter plots for each pair of random effects. It allows to identify correlations between random effects, which can then be introduced in the models for the probability distributions for the individual parameters.
Example
In the following example, one can see pairs of random effects estimated for all parameters of a one-compartment model with delayed first-order absorption and linear elimination estimated on the PK of warfarin data set. The estimators for random effects have been simulated from conditional distributions of individual random effects.
Visual guidelines
In addition to regression lines, Pearson correlation coefficients can been added to see the correlation between random effects, as well as spline interpolations.
Selection
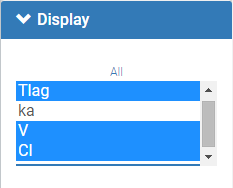
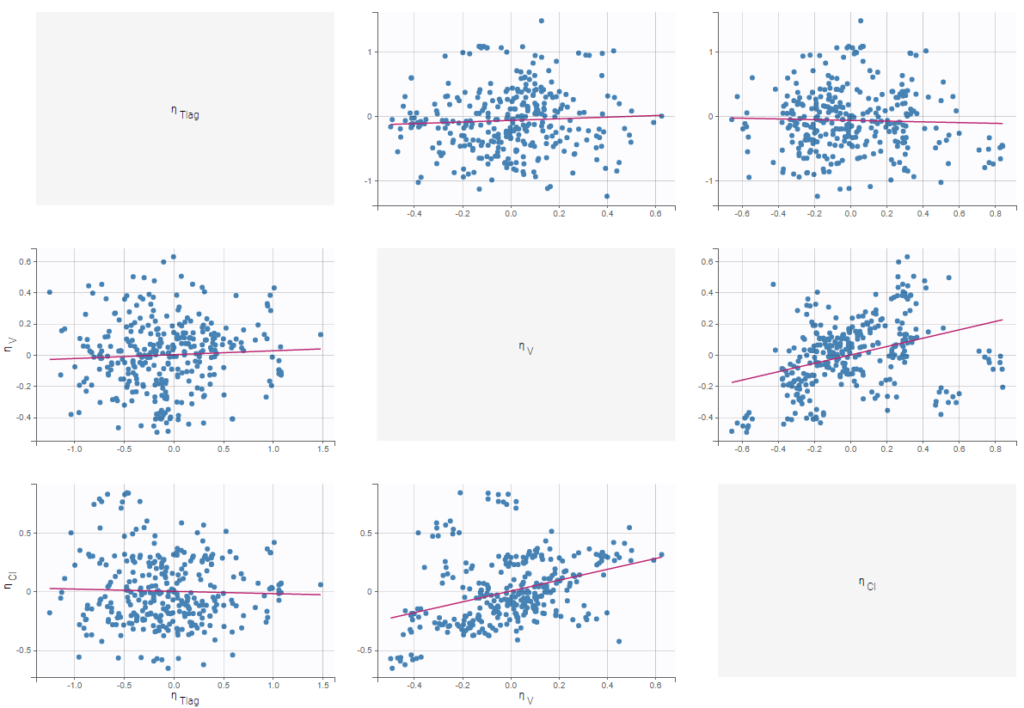
It is possible to select a subset of random effects, whose pairs of correlations are then displayed, as shown below. In the selection panel, a set of contiguous rows can be selected with a single extended click, or a set of non-contiguous rows can be selected with several clicks while holding the Ctrl key.
Highlight
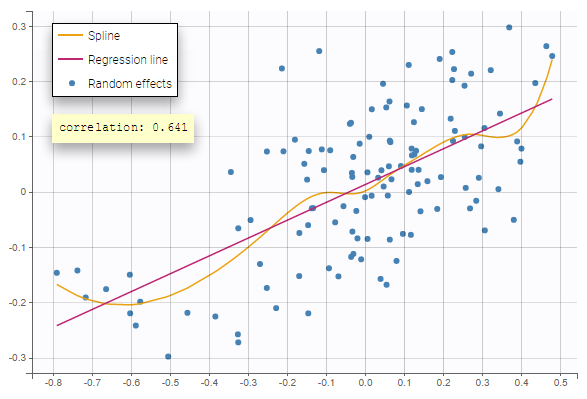
Similarly to other plots, hovering on a point provides information on the corresponding subject id, and highlights other points corresponding to the same individual, if multiple individual parameters have been simulated by sampling the conditional distribution.
On the figure below, we can see the same plot with only one parameter value per individual (left) or ten values (right). Notice that the correlation coefficient is more reliable when multiple parameters are available, as they take into account the uncertainty of individual parameters.
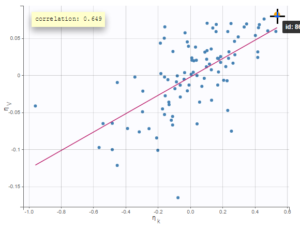 |
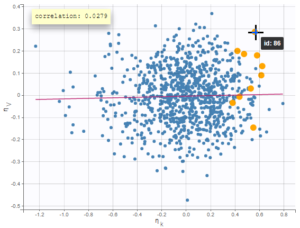 |
|---|
Stratification: coloring and filtering
Stratification can be applied by creating groups of covariate values. As can be seen below, these groups can then be colored (left) or filtered (right), allowing to check the effect of the covariate on the correlation between two parameters. The correlation coefficient is updated according to the filtering.
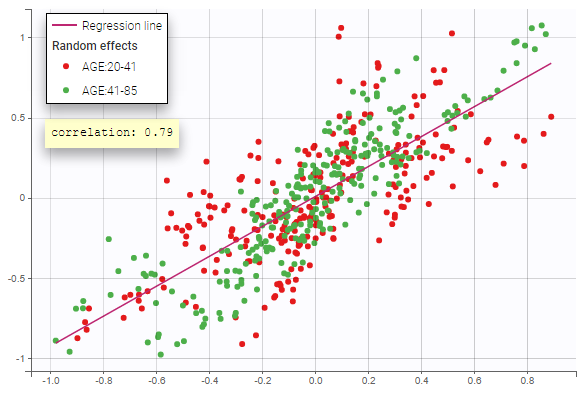 |
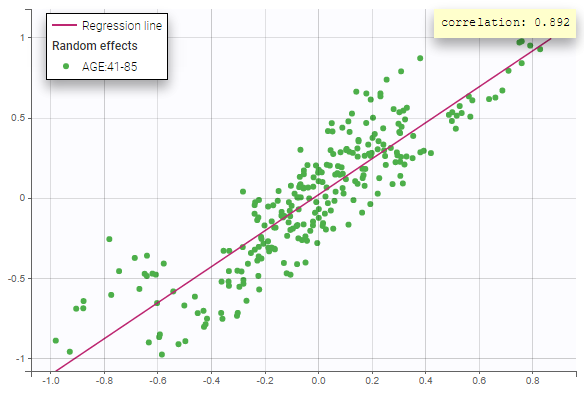 |
|---|
Settings
- General
- Legend and grid : add/remove the legend or the grid. There is only one legend for all plots.
- Correlation: display/hide the correlation coefficient associated with each scatter plot.
- Display
- Selection. The user can select some of the parameters to display only the corresponding scatter plots. A simple click selects one parameter, whereas multiple clicks while holding the Ctrl key selects a set of parameters.
- Individual estimates. The user can define which estimates are used for the definition of the individual parameters and thus for the random effects (conditional mean, conditional mode, simulated parameters)
- Visual cues. Add/remove the regression line or the spline interpolation.
By default, all scatter plots are proposed with simulated individual parameters.
Display in case of correlation in the statistical model
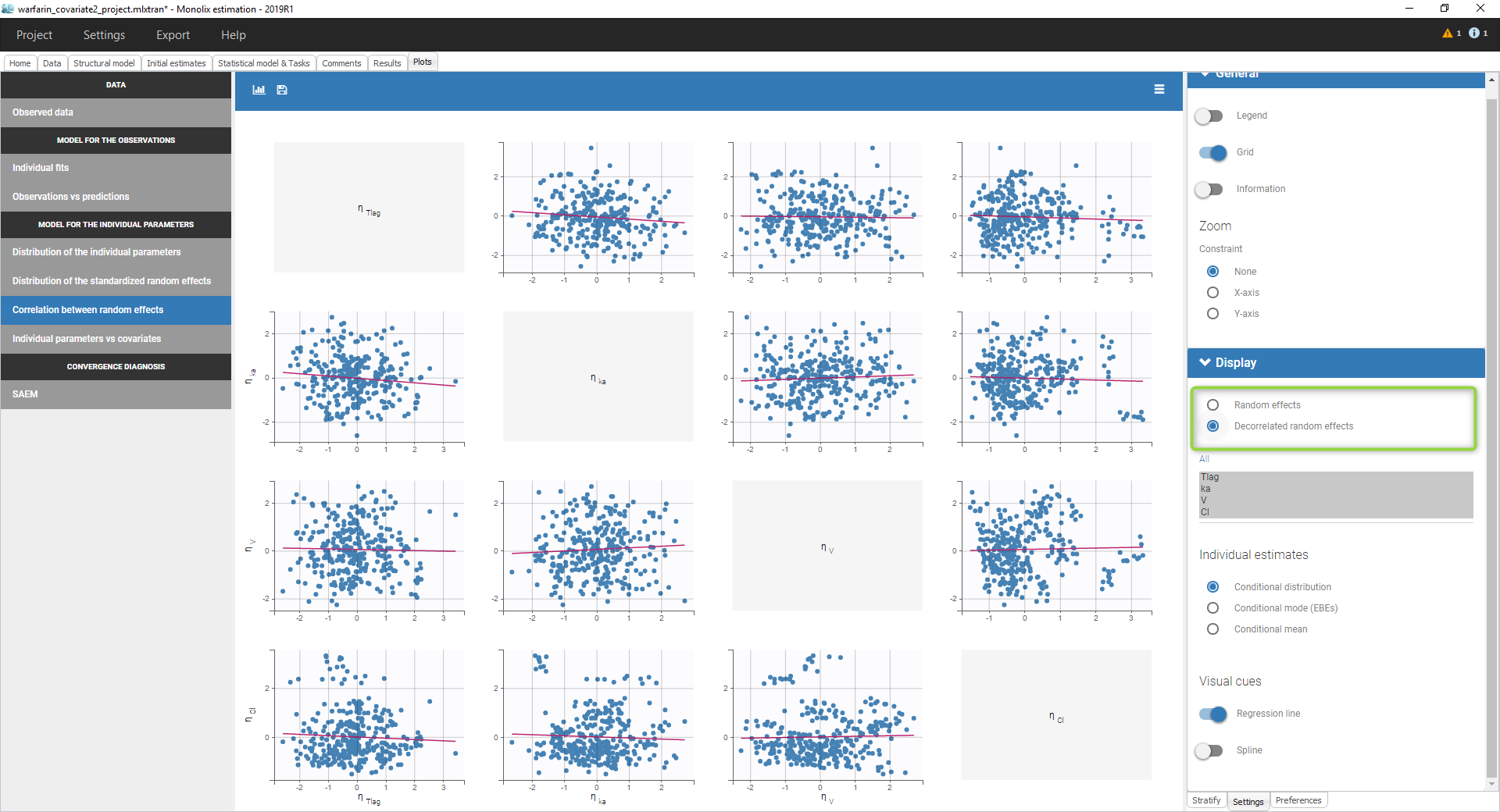
Starting from the 2019 version, when there is correlation in the statistical model, we propose to see the decorrelated random effects in order to see if some correlation remains. In that case, there is an option in the display to switch between the random effects and the decorrelated random effects as can be seen on the following figure. The methodology behind the calculation can be found here. The formula to calculate the decorrelated random effects \(\hat{\eta}_i\) from the random effects \(\eta_i\) and the estimated variance-covariance of the random effects \(\Omega\) is:
\(\hat{\eta}_i=\Omega^{-1/2}\times \eta_i \)
Display in case of IOV
Starting from the 2019 version, in case of IOV and if the conditional distribution is computed, we propose to display the by level of variability as can be seen in the following figure.
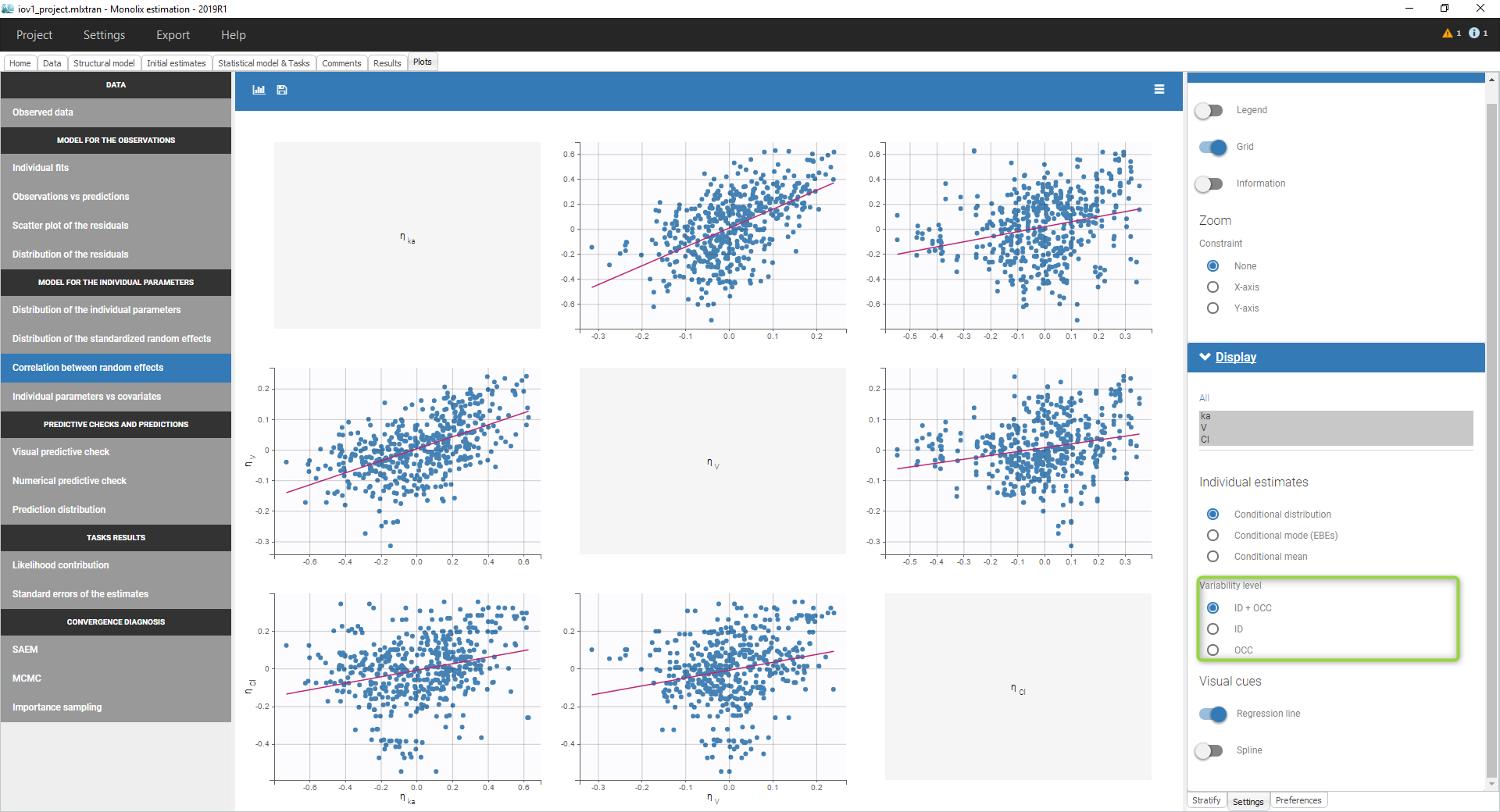 We can then display the correlation of the random effects for
We can then display the correlation of the random effects for
- the ID level,
- the OCC level (where only the parameters with variability on this level are displayed)
- the ID+OCC level corresponding to the addition of the levels
Notice that at least 2 parameters should have variability on the occasion level to have the correlation on the several level displayed.