Bounded parameter distribution

Bounded parameters in the interface

Starting from the 2019 version, it is possible to “extend” the logit distribution to be bounded in [a, b] rather than in [0, 1]. For that, set your parameter in a logit normal distribution. The setting button appear next to the distribution.

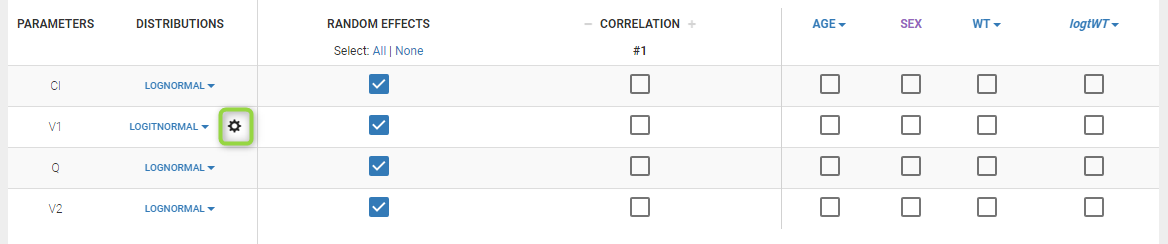
Clicking on it will allow to define your bounds as in the following figure.

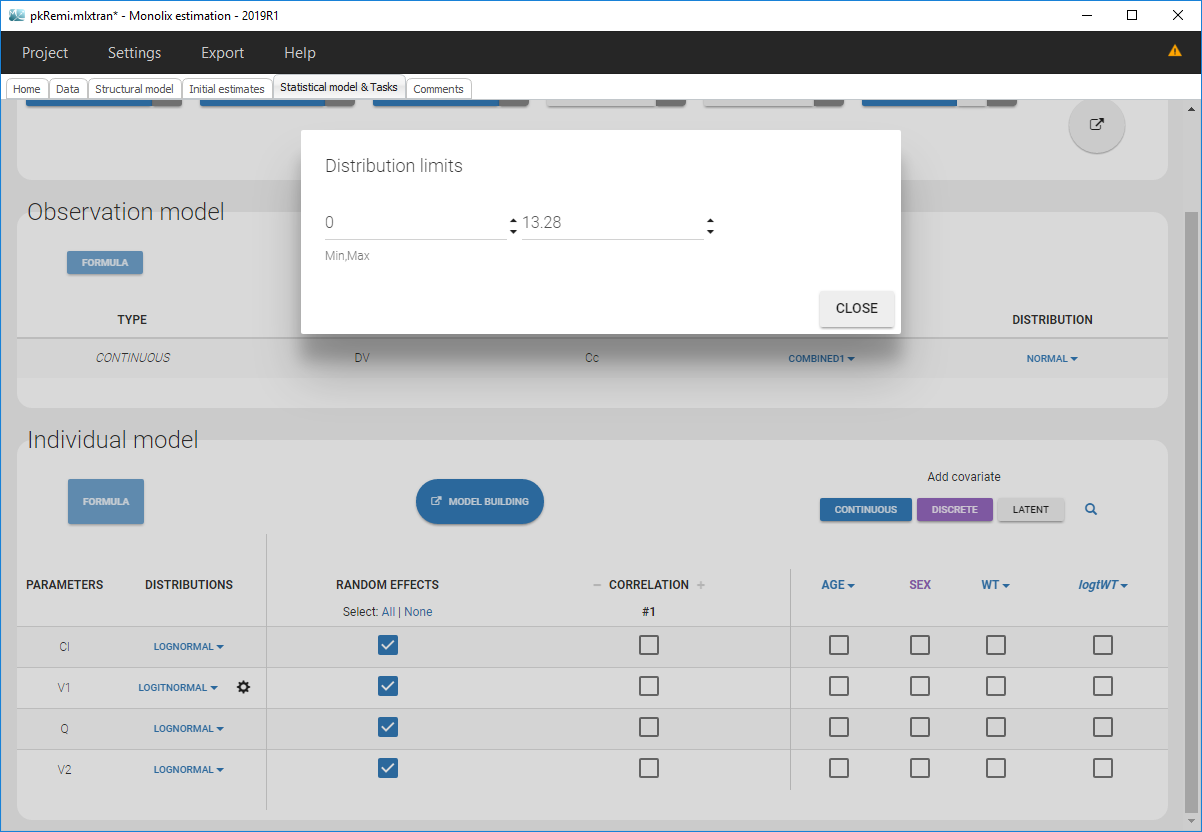
Notice that if your parameter initial value is not in [0, 1], the bounds are automatically adapted and the following warning message is proposed “The initial value of XX is greater than 1: the logit limit is adjusted”

Bounded parameters in the structural model

For versions of Monolix below 2019R1, a bounded parameter distribution, for example between a and b, can not be set directly through the interface, but have to be defined in two steps: (1) an auxiliary parameter and its distribution choice in the GUI, and (2) a transformation of the auxiliary parameter into the parameter of interest in the structural model file.

The same approach should be used in Monolix2019R1 to define a single bound (upper or lower).

Let’s take a simple PK example where a volume V is constrained. The structural model for this example is:

[LONGITUDINAL]
input = {V, k}
EQUATION:
; PK model definition
Cc = pkmodel(V, k)

Thus, to have a parameter V between two bounds a=1 and b=10, you have to define the structural model as below
```
[LONGITUDINAL]
input = {V_logit, k}
EQUATION:
; PK model definition
a = 1
b = 10
V_bound = a+V_logit*(b-a)
Cc = pkmodel(V=V_bound, k)
```
In the “Statistical model & Tasks” tab of the GUI, the distribution for V_logit should be set to LOGIT.

To have a parameter V larger than a=1 (with ‘a’ different from 0), you have to define the structural model as below
```
[LONGITUDINAL]
input = {V_log, k}
EQUATION:
; PK model definition
a = 1
V_bound = a+V_log
Cc = pkmodel(V=V_bound, k)
```
In the “Statistical model & Tasks” tab of the GUI, the distribution for V_log should be set to LOGNORMAL.

To have a parameter V smaller than b=10, you have to define the structural model as below
```
[LONGITUDINAL]
input = {V_log, k}
EQUATION:
; PK model definition
b = 10
V_bound = b-V_log
Cc = pkmodel(V=V_bound, k)
```
In the “Statistical model & Tasks” tab of the GUI, the distribution for V_log should be set to LOGNORMAL.

Notice that, using that transformation, you have to multiply the standard error of V_logit by (b-a) in the first case to have the standard error of the initial V_bound parameter. It is not necessary for the two other cases as it is an offset. In addition, you can output V_bound for each individual using the table statement.