When you select the estimation method as “Maximum A Posteriori Estimation” on a fixed effect, a window opens to define the prior distribution law as in the following:
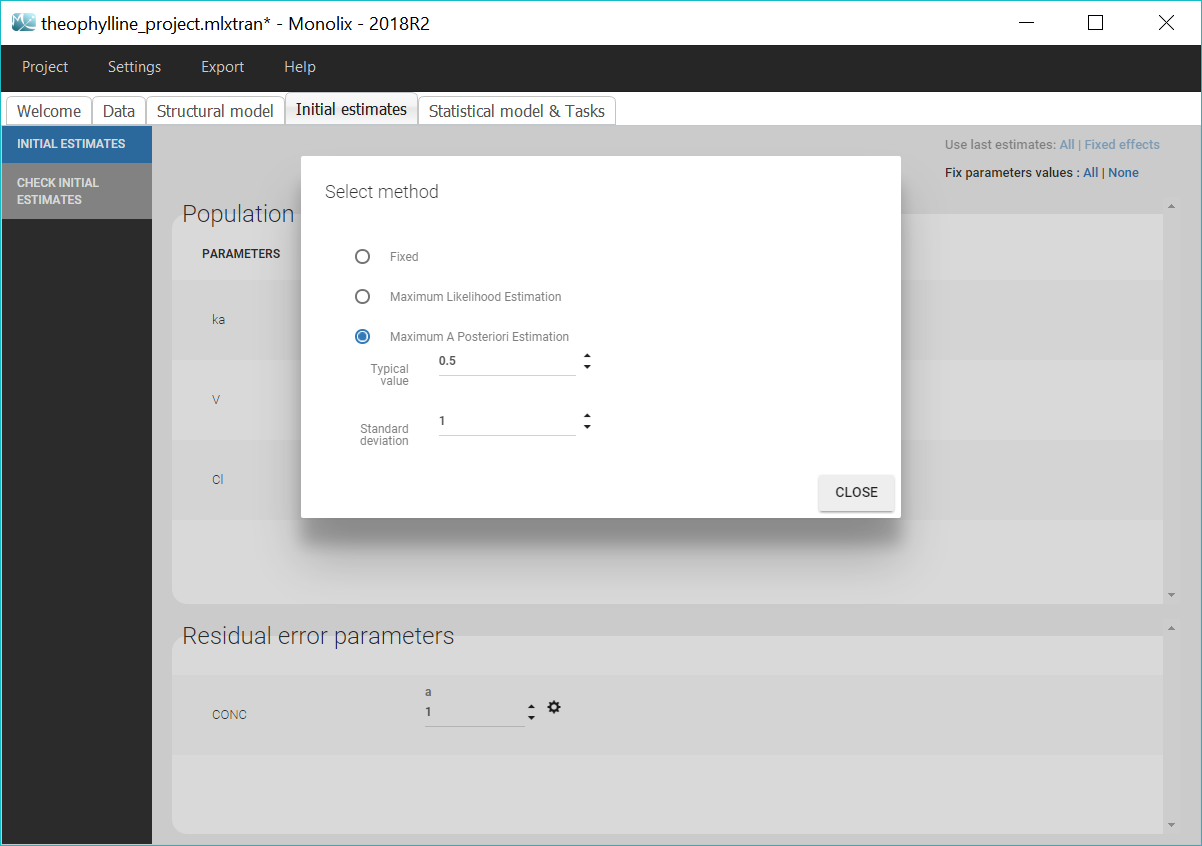
The prior distribution has the same distribution as the corresponding individual parameter. It is a fransformation T of a Gaussian distributed variable: \(\theta= T(Z)\) with \(\text{Z} \sim \mathcal{N} (\mu_Z, \sigma^2_Z)\). You must specify the typical value of \(\theta\) : \(\mu_Z = T^{-1}(\text{mean}_{\theta})\) and standard deviation of Z \(\sigma_Z\). By default, the current initial value will be used as typical value. Also, selecting a different typical value will set it automatically as initial value for the corresponding parameter.